题目内容
 若椭圆E1:
若椭圆E1:| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
| a1 |
| a2 |
| b1 |
| b2 |
(1)求经过点(2,
| 6 |
| x2 |
| 4 |
| y2 |
| 2 |
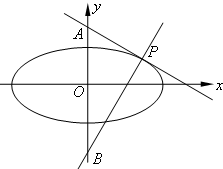
(2)设过原点的一条射线l分别与(1)中的两个椭圆交于A、B两点(其中点A在线段OB上),求|OA|+
| 1 |
| |OB| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设所求的椭圆方程为
+
=1,由题意得
,由此能求出椭圆方程.
(2)当射线与y轴重合时,|OA|+
=
;当射线不与坐标轴重合时,设其方程为y=kx(k≥0,x>0),设A(x1,y1),B(x2,y2),由已知条件推导出|OA|+
=
+
,由此能求出|OA|+
的最大值和最小值.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)当射线与y轴重合时,|OA|+
| 1 |
| |OB| |
5
| ||
| 4 |
| 1 |
| |OB| |
2
| ||
|
| ||
4
|
| 1 |
| |OB| |
解答:
解:(1)设所求的椭圆方程为
+
=1,
则由题意得
,解得
,…(3分)
∴所要求的椭圆方程为
+
=1.…(5分)
(2)①当射线与y轴重合时,
|OA|+
=
+
=
.…(6分)
②当射线不与坐标轴重合时,
由椭圆的对称性,我们仅考察A、B在第一象限的情形.
设其方程为y=kx(k≥0,x>0),设A(x1,y1),B(x2,y2),
由
,解得
,|OA|=
,…(7分)
由
,解得
,|OB|=
,…(8分)
|OA|+
=
+
,
令t=
,则由t=
=
=
,
知
<t≤2,…(10分)
|OA|+
=t+
,
记f(t)=t+
,则f(t)在(
,2]上是增函数,
∴f(
)<f(t)≤f(2),…(12分)
∴
<|OA|+
≤
,
由①②知,|OA|+
的最大值为
,
|OA|+
的最小值为
.…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
则由题意得
|
|
∴所要求的椭圆方程为
| x2 |
| 16 |
| y2 |
| 8 |
(2)①当射线与y轴重合时,
|OA|+
| 1 |
| |OB| |
| 2 |
| 1 | ||
2
|
5
| ||
| 4 |
②当射线不与坐标轴重合时,
由椭圆的对称性,我们仅考察A、B在第一象限的情形.
设其方程为y=kx(k≥0,x>0),设A(x1,y1),B(x2,y2),
由
|
|
2
| ||
|
由
|
|
4
| ||
|
|OA|+
| 1 |
| |OB| |
2
| ||
|
| ||
4
|
令t=
2
| ||
|
2
| ||
|
|
2+
|
知
| 2 |
|OA|+
| 1 |
| |OB| |
| 1 |
| 2t |
记f(t)=t+
| 1 |
| 2t |
| 2 |
∴f(
| 2 |
∴
| 5 |
| 4 |
| 2 |
| 1 |
| |OB| |
| 9 |
| 4 |
由①②知,|OA|+
| 1 |
| |OB| |
| 9 |
| 4 |
|OA|+
| 1 |
| |OB| |
5
| ||
| 4 |
点评:本题考查椭圆方程的求法,考查两线段和的最大值和最小值的求法,解题时要认真审题,注意换元法和函数的单调性的合理运用.

练习册系列答案
相关题目
函数f(x)=sinx(x∈[0,π]),在区间[0,π]上任取一点x0,则f(x0)≥
的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 椭圆C:
椭圆C:
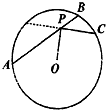 如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=
如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=