题目内容
已知直线
x-y+2m=0与圆x2+y2=n2相切,其中n,m∈N*,n-m<5,则满足条件的有序数对(m,n)的个数为 .
| 3 |
考点:直线与圆的位置关系,圆的切线方程
专题:直线与圆
分析:由直线和圆相切的性质可得,圆心到直线的距离等于半径,化简可得 2m=2n,再结合n-m<5,m,n∈N*,可得结论.
解答:
解:∵直线
x-y+2m=0与圆x2+y2=n2相切,
∴
=n,
∴2m=2n,
∵n-m<5,m,n∈N*,
∴m=1,2,3,4时,满足条件.
满足条件的有序实数对(m,n)有:(1,1)(2,2),(3,4),(4,8),
故答案为:4.
| 3 |
∴
| 2m |
| 2 |
∴2m=2n,
∵n-m<5,m,n∈N*,
∴m=1,2,3,4时,满足条件.
满足条件的有序实数对(m,n)有:(1,1)(2,2),(3,4),(4,8),
故答案为:4.
点评:本题考直线和圆的位置关系,考查点到直线的距离公式的应用,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
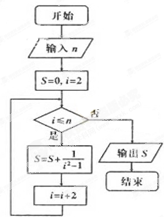
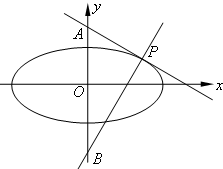 椭圆C:
椭圆C: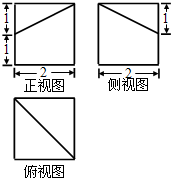
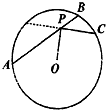 如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=
如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=