题目内容
若不等式|x-a|-|x|＜2-a2对x∈R恒成立，则实数a的取值范围是 ．
考点：绝对值不等式的解法
专题：不等式
分析：把2-a2看作一个参数，只需2-a2大于|x-a|-|x|的最大值．用a表示|x-a|-|x|的最大值，于是得到一个关于a的不等式，解此不等式即可．
解答：
解：∵不等式|x-a|-|x|＜2-a2对x∈R恒成立，
∴2-a2大于|x-a|-|x|的最大值，
根据绝对值的几何意义，
|x-a|表示数轴上的数x到a距离，|x|表示数轴上的数x到原点的距离，
∴|x-a|-|x|的最大值为|a-0|即|a|，
∴2-a2＞|a|，即|a|2+|a|-2＜0，得（|a|+2）（|a|-1）＜0，
解得0≤|a|＜1，∴-1＜a＜1．
故答案为：（-1，1）．
∴2-a2大于|x-a|-|x|的最大值，
根据绝对值的几何意义，
|x-a|表示数轴上的数x到a距离，|x|表示数轴上的数x到原点的距离，
∴|x-a|-|x|的最大值为|a-0|即|a|，
∴2-a2＞|a|，即|a|2+|a|-2＜0，得（|a|+2）（|a|-1）＜0，
解得0≤|a|＜1，∴-1＜a＜1．
故答案为：（-1，1）．
点评：本题属于不等式恒成立问题，有如下常见套路：
（1）若对x∈D，不等式a≥f（x）恒成立，则a≥[f（x）]max；
（2）若对x∈D，不等式a≤f（x）恒成立，则a≤[f（x）]min．
注：原不等中是否含有等于号，f（x）是否有最值，这都可能会影响到a能否取等号，对具体问题应具体分析，不能照搬套路．
（1）若对x∈D，不等式a≥f（x）恒成立，则a≥[f（x）]max；
（2）若对x∈D，不等式a≤f（x）恒成立，则a≤[f（x）]min．
注：原不等中是否含有等于号，f（x）是否有最值，这都可能会影响到a能否取等号，对具体问题应具体分析，不能照搬套路．
练习册系列答案
出彩同步大试卷系列答案
相关题目
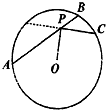如图，点P为圆O的弦AB上的任意点，连结PO，使∠OPC=90°，PC交圆于C，若AP=4，PC=3，则PB=