题目内容
 设椭圆
设椭圆| y2 |
| a2 |
| x2 |
| b2 |
(1)求椭圆的方程;
(2)求线段C,D中点Q的轨迹方程;
(3)若直线AC的斜率为1,在椭圆上求一点M,使三角形△MAC面积最大.
考点:轨迹方程,椭圆的标准方程,直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用短轴长为4,焦距为2,求出几何量,即可求椭圆的方程;
(2)利用点差法,可求线段C,D中点Q的轨迹方程;
(3)设平行于AC的直线方程为y=x+m,代入椭圆方程,利用△=0,求出m,即可在椭圆上求一点M,使三角形△MAC面积最大.
(2)利用点差法,可求线段C,D中点Q的轨迹方程;
(3)设平行于AC的直线方程为y=x+m,代入椭圆方程,利用△=0,求出m,即可在椭圆上求一点M,使三角形△MAC面积最大.
解答:
 解:(1)∵短轴长为4,焦距为2,
解:(1)∵短轴长为4,焦距为2,
∴b=2,c=1,
∴a=
=
,
∴椭圆方程为
+
=1.…(3分)
(2)设C(x1,y1),D(x2,y2),Q(x,y),则
+
=1①,
+
=1②
∵过点P(4,0)的直线l与椭圆交于C,D两点,线段C,D中点Q
∴①-②可得
•
=-
,即5x2-20x+4y2=0(0≤x≤1).…(8分)
(3)设平行于AC的直线方程为y=x+m,代入椭圆方程得9x2+8mx+4m2-20=0.
△=64m2-4•9•(4m2-20)=0,解得m=-3,m=3(舍).
把m=-3代入上式解得x=
,从而解得M(
,-
).…(11分)
把y=x+2代入椭圆方程整理得9x2+16x-4=0,
∴|AC|=
•
=
,AC边上高的最大值h=
,
∴△MAC面积最大值为
•
•
=
.…(14分)
 解:(1)∵短轴长为4,焦距为2,
解:(1)∵短轴长为4,焦距为2,∴b=2,c=1,
∴a=
| b2+c2 |
| 5 |
∴椭圆方程为
| y2 |
| 5 |
| x2 |
| 4 |
(2)设C(x1,y1),D(x2,y2),Q(x,y),则
| y12 |
| 5 |
| x12 |
| 4 |
| y22 |
| 5 |
| x22 |
| 4 |
∵过点P(4,0)的直线l与椭圆交于C,D两点,线段C,D中点Q
∴①-②可得
| y |
| x-4 |
| y |
| x |
| 5 |
| 4 |
(3)设平行于AC的直线方程为y=x+m,代入椭圆方程得9x2+8mx+4m2-20=0.
△=64m2-4•9•(4m2-20)=0,解得m=-3,m=3(舍).
把m=-3代入上式解得x=
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
把y=x+2代入椭圆方程整理得9x2+16x-4=0,
∴|AC|=
| 2 |
(-
|
20
| ||
| 9 |
| 5 | ||
|
∴△MAC面积最大值为
| 1 |
| 2 |
20
| ||
| 9 |
| 5 | ||
|
| 50 |
| 9 |
点评:本题考查椭圆的方程,考查点差法的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
已知三棱锥的三视图如图所示,则它的体积为( )
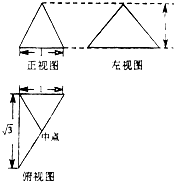

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
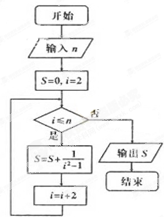
函数f(x)=sinx(x∈[0,π]),在区间[0,π]上任取一点x0,则f(x0)≥
的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
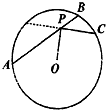 如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=
如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=