题目内容
已知a，b，c分别为△ABC内角A，B，C的对边，在△ABC中，b=
a，且sinB+cosB=0，则角A的大小为 ．
| 2 |
考点：正弦定理的应用
专题：解三角形
分析：首先，根据sinB+cosB=0，得到B=
，然后，结合正弦定理，得到sinA=
=
，从而，确定角A的大小．
| 3π |
| 4 |
| asinB |
| b |
| 1 |
| 2 |
解答：
解：∵sinB+cosB=0，
∴tanB=-1，
∵B∈（0，π），
∴B=
，
∵
=
，
∴sinA=
=
，
∵A∈（0，π），
∴A=
．
故答案为：
．
∴tanB=-1，
∵B∈（0，π），
∴B=
| 3π |
| 4 |
∵
| a |
| sinA |
| b |
| sinB |
∴sinA=
| asinB |
| b |
| 1 |
| 2 |
∵A∈（0，π），
∴A=
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：本题属于中档题，掌握特殊角的三角函数值是解题的关键，熟练应用正弦定理进行求解角度问题，是考试的热点问题．
练习册系列答案
优学名师名题系列答案
相关题目
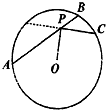如图，点P为圆O的弦AB上的任意点，连结PO，使∠OPC=90°，PC交圆于C，若AP=4，PC=3，则PB=
已知实数a，b，满足条件
，则事件：“2a-b＞0”发生的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|