题目内容
已知实数x、y满足:
,则z=y-
x的取值范围是 .
|
| 3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
解答:
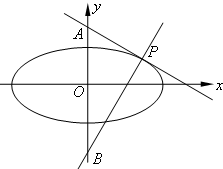
解:作出不等式组对应的平面区域(阴影部分),
由z=y-
x得y=
x+z,
平移直线y=
x,由图象可知当直线经过点C(2,0)时,直线y=
x+z的截距最小,此时z=-2
,
当直线y=
x+z与圆在第二象限相切时,直线y=
x+z的截距最大,
则d=
=
=2,解得z=±4,
故z的最大值为4,
则-2
≤z≤4,
故答案为:[-2
,4]

由z=y-
| 3 |
| 3 |
平移直线y=
| 3 |
| 3 |
| 3 |
当直线y=
| 3 |
| 3 |
则d=
| |z| | ||||
|
| |z| |
| 2 |
故z的最大值为4,
则-2
| 3 |
故答案为:[-2
| 3 |
点评:本题主要考查线性规划的应用以及直线和圆的位置关系,利用数形结合是解决本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
设a,b∈R,则“a+b>4”是“a>2且b>2”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
 椭圆C:
椭圆C: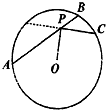 如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=
如图,点P为圆O的弦AB上的任意点,连结PO,使∠OPC=90°,PC交圆于C,若AP=4,PC=3,则PB=