题目内容
2.若关于x的方程4x-(a+3)2x+1=0有实数解,则实数a的取值范围是[-1,+∞).分析 分离变量,然后利用基本不等式求解表达式的最值,即可求出a的范围.
解答 解:关于x的方程4x-(a+3)2x+1=0有实数解,即a+3=2x+$\frac{1}{{2}^{x}}$≥2$\sqrt{{2}^{x}•\frac{1}{{2}^{x}}}$=2,当且仅当x=0时取等号.
∴a≥-1,
所以a的范围为[-1,+∞)
故答案为:[-1,+∞).
点评 本题考查指数函数的定义、基本不等式求最值问题,同时考查转化思想,比较基础.

练习册系列答案
相关题目
12.已知圆P的半径等于椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1的长轴长,圆心是抛物线y2=4$\sqrt{2}$x的焦点,经过点M(-$\sqrt{2}$,1)的直线1将圆P分成两段弧,则劣弧长度的最小值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | 2π | D. | 4π |
11.如图所示的程序框图,输出的值为( )
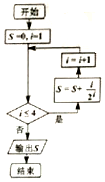

| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |
12.已知函数$f(x)=3cos(ωx+\frac{π}{3})(ω>0)$和g(x)=2sin(2x+φ)+1的图象的对称轴完全相同,若$x∈[0,\frac{π}{3}]$,则f(x)的取值范围是( )
| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |