题目内容
(理科做)
|x2-2x|dx= .
| ∫ | 4 0 |
考点:定积分
专题:导数的概念及应用
分析:将:∫04|x2-2x|dx转化成∫02(2x-x2)dx+∫24(x2-2x)dx,然后根据定积分的定义先求出被积函数的原函数,然后求解即可.
解答:
解:∫04|x2-2x|dx
=∫02(2x-x2)dx+∫24(x2-2x)dx
=(x2-
x3)
+(
x3-x2)
=(4-
×8)+(
×64-16)-(
×8-4)
=8,
故答案为:8.
=∫02(2x-x2)dx+∫24(x2-2x)dx
=(x2-
| 1 |
| 3 |
| | | 2 0 |
| 1 |
| 3 |
| | | 4 2 |
=(4-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=8,
故答案为:8.
点评:本题主要考查了定积分,定积分运算是求导的逆运算,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
相关题目
已知关于x的不等式
<1的解集为{x|x<1或x>3},则a的值为( )
| ax |
| x-1 |
| A、3 | ||
B、
| ||
C、-
| ||
D、
|
经过抛物线x2=4y的焦点和双曲线
-
=1的右焦点的直线方程为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、3x+y-3=0 |
| B、x+3y-3=0 |
| C、x+48y-3=0 |
| D、48x+y-3=0 |
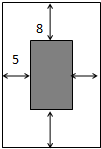 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?