题目内容
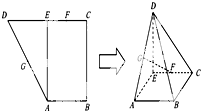 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.(1)求证:AE⊥平面CDE;
(2)求证:FG∥平面BCD;
(3)在线段DC上找一点R,使得平面AER⊥平面DCB,并说明理由.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由已知得DE⊥AE,AE⊥EC.根据线面垂直的判定定理,我们可得AE⊥平面CDE;
(2)取AB中点H,连接GH,FH,由三角形中位线定理,我们易得到GH∥BD,FH∥BC,由面面平行的判定定理得到面FHG∥面BCD,再由面面平行的定义,得到FG∥平面BCD;
(3)取线段DC中点R,则平面AER⊥平面DCB,根据线面垂直判定定理,及面面垂直判定定理,得到结论.
(2)取AB中点H,连接GH,FH,由三角形中位线定理,我们易得到GH∥BD,FH∥BC,由面面平行的判定定理得到面FHG∥面BCD,再由面面平行的定义,得到FG∥平面BCD;
(3)取线段DC中点R,则平面AER⊥平面DCB,根据线面垂直判定定理,及面面垂直判定定理,得到结论.
解答:
证明:(1)由已知得DE⊥AE,AE⊥EC.
∵DE∩EC=E,DE、EC?平面DCE.…(2分)
∴AE⊥平面CDE.…(4分)
(1)取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD.
∴面FHG∥面BCD,∵GF?面FHG
∴GF∥平面BCD.…(8分)
(3)取线段DC中点R,则平面AER⊥平面DCB
∵在△DEC中,DE=EC,R为DC中点
∴ER⊥DC …(9分)
∵AE⊥平面CDE,DC?平面DCE
∴AE⊥DC…(10分)
又ER∩AE=E,AE、ER?平面AER.
∴DC⊥平面AER…(11分)
∵DC?平面DCB
∴平面AER⊥平面DCB
即 取DC中点R时,有平面AER⊥平面DCB …(12分)
∵DE∩EC=E,DE、EC?平面DCE.…(2分)
∴AE⊥平面CDE.…(4分)
(1)取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD.
∴面FHG∥面BCD,∵GF?面FHG
∴GF∥平面BCD.…(8分)
(3)取线段DC中点R,则平面AER⊥平面DCB
∵在△DEC中,DE=EC,R为DC中点
∴ER⊥DC …(9分)
∵AE⊥平面CDE,DC?平面DCE
∴AE⊥DC…(10分)
又ER∩AE=E,AE、ER?平面AER.
∴DC⊥平面AER…(11分)
∵DC?平面DCB
∴平面AER⊥平面DCB
即 取DC中点R时,有平面AER⊥平面DCB …(12分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间直线与平面之间平行及垂直的判定定理、性质定理、定义、几何特征是解答此类问题的关键.

练习册系列答案
相关题目
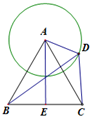 △ABC是边长为2的等边三角形,D是以A为圆心,半径为1的圆上任意一点,如图所示,则
△ABC是边长为2的等边三角形,D是以A为圆心,半径为1的圆上任意一点,如图所示,则| BD |
| CD |
A、3+
| ||
B、3-
| ||
C、3-2
| ||
D、3+2
|
对于两个变量y和x进行线性相关检验,已知n是 观察值组数,r是相关系数,且已知:①n=7,r=0,9533;②n=15,r=0.301,③n=17,r=0.9991,④n=3,r=0.9950,则变量y和x具有线性相关关系的是( )
| A、①和② | B、①和③ |
| C、②和④ | D、③和④ |
已知关于x的不等式
<1的解集为{x|x<1或x>3},则a的值为( )
| ax |
| x-1 |
| A、3 | ||
B、
| ||
C、-
| ||
D、
|
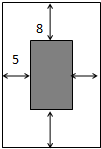 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?