题目内容
定义在R上的奇函数f（x）在[-1，0]上单调递减，则下列关系式正确的是（ ）
| A、0＜f（1）＜f（-1） |
| B、f（-1）＜f（1）＜0 |
| C、f（1）＜0＜f（-1） |
| D、f（-1）＜0＜f（1） |
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系即可得到结论．
解答：
解：∵奇函数f（x）在[-1，0]上单调递减，
∴函数f（x）在[0，1]上单调递减，
即函数f（x）在[-1，1]上单调递减，
则f（1）＜0＜f（-1），
故选：C
∴函数f（x）在[0，1]上单调递减，
即函数f（x）在[-1，1]上单调递减，
则f（1）＜0＜f（-1），
故选：C
点评：本题主要考查函数值的大小比较，根据函数奇偶性和单调性之间的关系即可得到结论．
练习册系列答案
阅读快车系列答案
相关题目
某地铁的到站时间间隔是5分钟．某人进站到达列车门口等车时间超过2分钟的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
两位老师和两位同学站成一排合影，则两位老师至少有一人站在两端的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
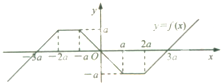（理做）如图所示，函数y=f（x）的图象由两条射线和三条线段组成，若?x∈R，f（x）＞f（x-2），则正实数的取值范围是