题目内容
两位老师和两位同学站成一排合影,则两位老师至少有一人站在两端的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:先求出2位老师,2位学生站成一排合影,没有任何要求的站法,再求出每位老师都不站在两端的站法,根据对立事件的概率公式求得.
解答:
解:2位老师,2位学生站成一排合影,没有任何要求的排列是A44=24种,
每位老师都不站在两端,则两端只能是2名学生站,有A22A22=4种,
根据古典概型的概率公式可得,有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是P=
=
,
故两位老师至少有一人站在两端的概率是1-
=
故选A.
每位老师都不站在两端,则两端只能是2名学生站,有A22A22=4种,
根据古典概型的概率公式可得,有2位老师,2位学生站成一排合影,则每位老师都不站在两端的概率是P=
| 4 |
| 24 |
| 1 |
| 6 |
故两位老师至少有一人站在两端的概率是1-
| 1 |
| 6 |
| 5 |
| 6 |
故选A.
点评:本题主要考查了古典概型的概率问题,关键是利用排列组合求出基本事件,属于基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
不等式ax2-x-c>0的解集为{x|-2<x<1},则函数y=ax2+x-c的零点为( )
| A、(-1,0)和(2,0) |
| B、(-1,0) |
| C、(2,0) |
| D、-1和2 |
定义在R上的奇函数f(x)在[-1,0]上单调递减,则下列关系式正确的是( )
| A、0<f(1)<f(-1) |
| B、f(-1)<f(1)<0 |
| C、f(1)<0<f(-1) |
| D、f(-1)<0<f(1) |
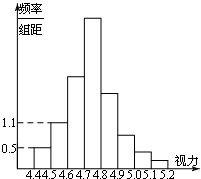 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )| A、77,0.53 |
| B、70,0.32 |
| C、77,5.3 |
| D、70,3.2 |
(文做)函数f(x)=(x-1)(x-2)+(x-2)(x-3)+(x-3)(x-1)的两个零点分别位于区间( )
| A、(2,3)和(3,+∞)内 |
| B、(-∞,1)和(1,2)内 |
| C、(1,2)和(2,3)内 |
| D、(-∞,1)和(3,+∞)内 |