题目内容
已知a,b,c为△ABC的三个内角A,B,C的对边,满足acosB+bcosA=csinC,向量
=(
,-1),
=(cosA,sinA).若
⊥
,则角B= .
| m |
| 3 |
| n |
| m |
| n |
考点:正弦定理,平面向量的综合题
专题:计算题,平面向量及应用
分析:由向量数量积的意义,由
⊥
,可得
cosA-sinA=0,进而可得A,再根据正弦定理,可得sinAcosB+sinBcosA=sinC sinC,结合和差公式的正弦形式,化简可得sinC=sin2C,可得C,由A、C的大小,可得B.
| m |
| n |
| 3 |
解答:
解:根据题意,
⊥
,∴
cosA-sinA=0,
∴A=
,
∵acosB+bcosA=csinC
由正弦定理可得,sinAcosB+sinBcosA=sinCsinC,
又由sinAcosB+sinBcosA=sin(A+B)=sinC,
化简可得,sinC=sin2C,
∴C=
,
∴B=
.
故答案为:
.
| m |
| n |
| 3 |
∴A=
| π |
| 3 |
∵acosB+bcosA=csinC
由正弦定理可得,sinAcosB+sinBcosA=sinCsinC,
又由sinAcosB+sinBcosA=sin(A+B)=sinC,
化简可得,sinC=sin2C,
∴C=
| π |
| 2 |
∴B=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查向量数量积的应用,判断向量的垂直,以及两角和正弦函数的应用,解题时,注意向量的正确表示方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( )
A、(-
| ||
B、[-
| ||
| C、[-2,1) | ||
| D、(-2,1) |
若f(x)=3sin(ωx+φ)(ω>0,|φ|<
)的周期为π且图象关于x=
对称,则( )
| π |
| 2 |
| 2π |
| 3 |
A、f(x)的图象过点(0,
| ||||
B、f(x)在[
| ||||
| C、将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象 | ||||
D、f(x)的一个对称中心是(
|
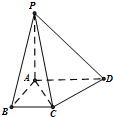 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为