题目内容
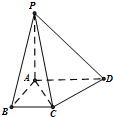如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠ABC=90°，AD∥BC，且PA=AD=2，AB=BC=1，则PD与平面PAC所成的角大小为考点：直线与平面所成的角
专题：空间角
分析：由AC⊥CD，又PA⊥平面ABCD，得PA⊥DC，DC⊥面PAC，从而PD与平面PAC所成的角为∠DPC，由此能求出结果．
解答：
解：由题意，AC=
，
又AD=2，∴AC⊥CD，
又PA⊥平面ABCD，∴PA⊥DC，∴DC⊥面PAC，
∴PD与平面PAC所成的角为∠DPC，
∴tan∠DPC=
=
=
．
∴∠DPC=30°．
∴PD与平面PAC所成的角大小为30°．
故答案为：30°．
| 2 |
又AD=2，∴AC⊥CD，
又PA⊥平面ABCD，∴PA⊥DC，∴DC⊥面PAC，
∴PD与平面PAC所成的角为∠DPC，
∴tan∠DPC=
| DC |
| PC |
| ||
|
| ||
| 3 |
∴∠DPC=30°．
∴PD与平面PAC所成的角大小为30°．
故答案为：30°．
点评：本题考查空间角，考查学生分析解决问题的能力，正确运用线面平行的判定是关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
对一个边长互不相等的凸n（n≥3）边形的边染色，每条边可以染红、黄、蓝三种颜色中的一种，但是不允许相邻的边有相同的颜色．所有不同的染色方法记为P（n），则P（n）=已知函数f（x）=
（x∈（0，
）），则f（x）的最小值为（ ）
| sinx+cosx |
| sinxcosx |
| π |
| 2 |
A、
| ||
B、2
| ||
C、4
| ||
D、6
|
函数y=log3（x-1）的定义域为（ ）
| A、R |
| B、（-∞，1）∪（1，∞） |
| C、（-∞，1） |
| D、（1，∞） |