题目内容
1.已知函数f(x)=$\frac{a}{{x}^{2}}$+21nx,若当a>0时,f(x)≥2恒成立,则实数a的取值范围是a≥e.分析 不等式可整理为a≥2x2(1-lnx)恒成立,只需求出右式的最大值即可,构造函数令h(x)=2x2(1-lnx),求出导函数h'(x)=2x(1-2lnx),
利用导函数求出原函数的最大值即可.
解答 解:若当a>0时,f(x)≥2恒成立,
∴a≥2x2(1-lnx)恒成立,
令h(x)=2x2(1-lnx),h'(x)=2x(1-2lnx),
∴当x∈(0,${e}^{\frac{1}{2}}$)时,h(x)>0,h(x)递增,
当x∈(${e}^{\frac{1}{2}}$,+∞)时,h(x)<0,h(x)递减,
∴h(x)的最大值为h(${e}^{\frac{1}{2}}$)=e,
∴a≥e.
点评 考查了恒成立问题的转化和构造函数,利用导函数判断函数最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.$\sqrt{3}$tan12°+$\sqrt{3}$tan18°+tan12°•tan18°的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 0 | D. | 1 |
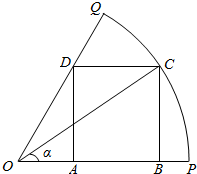 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,