题目内容
13.已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.(1)若f(1)≤8,求实数a的取值范围;
(2)设a=1,对任意的x1,x2∈(-1,0),关于m的不等式|$\frac{{x}_{1}}{f({x}_{1})}$-g(x2)|<m恒成立,求实数m的取值范围;
(3)设H1(x)=max{f(x,g(x)},H2(x)=min{f(x),g(x)},其中max{p,q}表示p,q中的较大者,min{p,q}表示p,q中的较小者;记H1(x)的最小值为A,H2(x)的最大值为B,求A-B的值.
分析 (1)由题意可得a2-2a-11≤0,运用二次不等式的解法可得范围;
(2)分别求得$\frac{x}{f(x)}$,g(x)的范围,由题意可得|$\frac{{x}_{1}}{f({x}_{1})}$-g(x2)|max<m,即可得到所求范围;
(3)在同一坐标系中画出f(x)与g(x)的图象,由图象及H1(x)的定义知H1(x)的最小值是f(a+2),H2(x)的最大值为g(a-2),进而可得答案.
解答 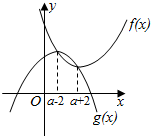 解:(1)f(1)≤8,即为a2-2a-11≤0,
解:(1)f(1)≤8,即为a2-2a-11≤0,
解得1-2$\sqrt{3}$≤a≤1+2$\sqrt{3}$;
(2)当a=1时,f(x)=x2-6x+1,g(x)=-x2-2x+7,
即有$\frac{x}{f(x)}$=$\frac{x}{{x}^{2}-6x+1}$=$\frac{1}{x+\frac{1}{x}-6}$,由-1<x<0,可得x+$\frac{1}{x}$<-2,
即有$\frac{x}{f(x)}$∈(-$\frac{1}{8}$,0);
g(x)=-x2-2x+7=-(x+1)2+8∈(7,8),
由m的不等式|$\frac{{x}_{1}}{f({x}_{1})}$-g(x2)|<m恒成立,
由|$\frac{{x}_{1}}{f({x}_{1})}$-g(x2)|<8+$\frac{1}{8}$=$\frac{65}{8}$,
则m≥$\frac{65}{8}$;
(3)令f(x)=g(x),
即x2-2(a+2)x+a2=-x2+2(a-2)x-a2+8,
即x2-2ax+a2-4=0,
解得x=a+2或x=a-2.
f(x)与g(x)的图象如图.
由图象及H1(x)的定义知H1(x)的最小值是f(a+2),
H2(x)的最大值为g(a-2),
则A-B=f(a+2)-g(a-2)
=(a+2)2-2(a+2)2+a2+(a-2)2-2(a-2)2+a2-8=-16.
点评 本题主要考查了二次函数的图象与性质、函数最值的应用等,考查了数形结合的思想,考查运算能力,属于中档题.

| A. | 和两条异面直线都相交的两条直线是异面直线 | |
| B. | 和两条异面直线都相交于不同点的两条直线是异面直线 | |
| C. | 和两条异面直线都垂直的直线是异面直线的公垂线 | |
| D. | 若a、b是异面直线,b、c是异面直线,则a、c是异面直线 |
| A. | 偶函数且它的图象关于点(π,0)对称 | |
| B. | 偶函数且它的图象关于点($\frac{3π}{2}$,0)对称 | |
| C. | 奇函数且它的图象关于点($\frac{3π}{2}$,0)对称 | |
| D. | 奇函数且它的图象关于点(π,0)对称 |
| A. | $\frac{2}{21}$ | B. | $\frac{4}{21}$ | C. | $\frac{5}{21}$ | D. | $\frac{11}{42}$ |