题目内容
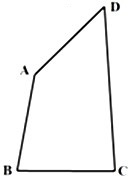 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=| 3 |
(Ⅰ)写出cosC与cosA的关系式;
(Ⅱ)设△BCD和△ABD的面积分别为S和T,求S2+T2的最大值.
考点:余弦定理
专题:三角函数的求值
分析:(Ⅰ)在三角形BCD和三角形BCD中,利用余弦定理表示出BD2,两者相等表示即可得到cosC与cosA的关系式;
(Ⅱ)利用三角形面积公式变形出S与T,进而表示出S2+T2,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出S2+T2的最大值.
(Ⅱ)利用三角形面积公式变形出S与T,进而表示出S2+T2,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出S2+T2的最大值.
解答:
解:(Ⅰ)连接BD,
∵CD=
,AB=BC=DA=1,
∴在△BCD中,利用余弦定理得:BD2=BC2+CD2-2BC•CDcosC=4-2
cosC;
在△ABD中,BD2=2-2cosA,
∴4-2
cosC=2-2cosA,
则cosA=
cosC-1;
(Ⅱ)S=
BC•CD•sinC=
sinC,T=
AB•ADsinA=
sinA,
∵cosA=
cosC-1,
∴S2+T2=
sin2C+
sin2A=
(1-cos2C)+
(1-cos2A)=-
cos2C+
cosC+
=-
(cosC-
)2+
,
则当cosC=
时,S2+T2有最大值
.
∵CD=
| 3 |
∴在△BCD中,利用余弦定理得:BD2=BC2+CD2-2BC•CDcosC=4-2
| 3 |
在△ABD中,BD2=2-2cosA,
∴4-2
| 3 |
则cosA=
| 3 |
(Ⅱ)S=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵cosA=
| 3 |
∴S2+T2=
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| ||
| 6 |
| 7 |
| 8 |
则当cosC=
| ||
| 6 |
| 7 |
| 8 |
点评:此题考查了余弦定理,三角形面积公式,同角三角函数间的基本关系,以及二次函数的性质,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
下列命题中的真命题是( )
| A、若a>b>0,a>c,则a2>bc | ||||
B、若a>b>c,则
| ||||
| C、若a>b,n∈N*,则an>bn | ||||
| D、若a>b>0,则1na<1nb |
 已知椭圆C1:
已知椭圆C1: 已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足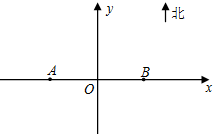 为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.
为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.