题目内容
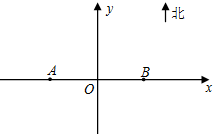 为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.
为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.(Ⅰ)以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系,求观测区域边界曲线的方程;
(Ⅱ)某日上午7时,观测站B发现在其正东10海里的C处,有一艘轮船正以每小时8海里的速度向北偏西45°方向航行,问该轮船大约在什么时间离开观测区域?(参考数据:
| 2 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:Ⅰ)以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系,题意可知:考察区域边界曲线是以A,B为焦点的椭圆,设出椭圆方程,利用相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域,即可得到观测区域边界曲线的方程;
(Ⅱ)设轮船在观测区域内航行的时间为t小时,航线与区域边界的交点为C、D,可得直线CD方程,与椭圆方程联立,求出|CD|,即可求出结论.
(Ⅱ)设轮船在观测区域内航行的时间为t小时,航线与区域边界的交点为C、D,可得直线CD方程,与椭圆方程联立,求出|CD|,即可求出结论.
解答:
 解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)
解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)
(Ⅰ)依题意可知:考察区域边界曲线是以A,B为焦点的椭圆,…(2分)
设椭圆方程为:
+
=1(a>b>0),
则
,…(4分)
解得a=20,b=10
,…(5分)
∴观测区域边界曲线的方程为:
+
=1.…(6分)
(Ⅱ)设轮船在观测区域内航行的时间为t小时,航线与区域边界的交点为C、D,
∵C(20,0),kCD=tan135°=-1,
∴直线CD方程:y=-x+20.…(7分)
联立方程
,整理得:7x2-160x+400=0,…(8分)
解得x1=20,x2=
…(9分)
∴|CD|=
•|20-
|=
≈24…(11分)
∴t=
=3(小时).
∴轮船大约在当日上午10时离开观测区域.…(12分)
 解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)
解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)(Ⅰ)依题意可知:考察区域边界曲线是以A,B为焦点的椭圆,…(2分)
设椭圆方程为:
| x2 |
| a2 |
| y2 |
| b2 |
则
|
解得a=20,b=10
| 3 |
∴观测区域边界曲线的方程为:
| x2 |
| 400 |
| y2 |
| 300 |
(Ⅱ)设轮船在观测区域内航行的时间为t小时,航线与区域边界的交点为C、D,
∵C(20,0),kCD=tan135°=-1,
∴直线CD方程:y=-x+20.…(7分)
联立方程
|
解得x1=20,x2=
| 20 |
| 7 |
∴|CD|=
| 2 |
| 20 |
| 7 |
| 120 |
| 7 |
| 2 |
∴t=
| 24 |
| 8 |
∴轮船大约在当日上午10时离开观测区域.…(12分)
点评:本题主要考查直线、圆、椭圆等基础知识及直线与椭圆的位置关系;考查运算求解、抽象概括能力、应用意识,化归与转化思想.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知集合A={1,2},B={1,a,b},则“a=2”是“A⊆B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设变量x,y满足约束条件
,则目标函数z=4x+y的最小值为( )
|
| A、1 | B、4 | C、11 | D、12 |
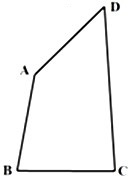 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=