题目内容
已知函数f（x）=2sin（x+
）cosx．
（Ⅰ）若x∈[0，
]，求f（x）的取值范围；
（Ⅱ）设△ABC的内角A、B、C所对的边分别为a、b、c，已知A为锐角，f（A）=
，b=2，c=3，求cos（A-B）的值．
| π |
| 3 |
（Ⅰ）若x∈[0，
| π |
| 2 |
（Ⅱ）设△ABC的内角A、B、C所对的边分别为a、b、c，已知A为锐角，f（A）=
| ||
| 2 |
考点：三角函数中的恒等变换应用,正弦定理
专题：三角函数的图像与性质,解三角形
分析：（Ⅰ）利用三角函数中的恒等变换应用可求得f（x）=sin（2x+
）+
，利用x∈[0，
]，可求得2x+
∈[
，
]，从而可求得f（x）的取值范围；
（Ⅱ）依题意可求得sin（2A+
）=0，A为锐角，可知A=
，b=2，c=3，利用余弦定理可求得a=
，继而可求得sinB及cosB的值，利用两角差的余弦可得cos（A-B）的值．
| π |
| 3 |
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
（Ⅱ）依题意可求得sin（2A+
| π |
| 3 |
| π |
| 3 |
| 7 |
解答：
解：（Ⅰ）f(x)=(sinx+
cosx)cosx=sinxcosx+
cos2x
=
sin2x+
cos2x+
=sin(2x+
)+
…．（4分）
∵x∈[0，
]，
∴2x+
∈[
，
]，-
≤sin(2x+
)≤1．
∴f(x)∈[0， 1+
]． …．（7分）
（Ⅱ）由f(A)=sin(2A+
)+
=
，得sin（2A+
）=0，
又A为锐角，故A=
，又b=2，c=3，
∴a2=4+9-2×2×3×cos
=7，解得a=
． …．（10分）
由
=
，得sinB=
，又b＜a，从而B＜A，cosB=
．
∴cos(A-B)=cosAcosB+sinAsinB=
•
+
•
=
…（14分）
| 3 |
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 3 |
| ||
| 2 |
∵x∈[0，
| π |
| 2 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| ||
| 2 |
| π |
| 3 |
∴f(x)∈[0， 1+
| ||
| 2 |
（Ⅱ）由f(A)=sin(2A+
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
又A为锐角，故A=
| π |
| 3 |
∴a2=4+9-2×2×3×cos
| π |
| 3 |
| 7 |
由
| a |
| sinA |
| b |
| sinB |
| ||
|
| 2 | ||
|
∴cos(A-B)=cosAcosB+sinAsinB=
| 1 |
| 2 |
| 2 | ||
|
| ||
| 2 |
| ||
|
5
| ||
| 14 |
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的单调性与值域，考查正弦定理的应用，属于中档题．
练习册系列答案
活力课时同步练习册系列答案
相关题目
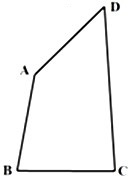如图，在凸四边形ABCD中，C，D为定点，CD=
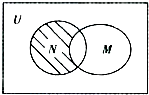已知集合M={x|x2-2x≤0}，N={x|