题目内容
在平面直角坐标系xOy中,动点P(x,y)到F(0,1)的距离比到直线y=-2的距离小1.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)过点E(0,-4)的直线与轨迹W交于两点A,B,点D是点E关于x轴的对称点,点A关于y轴的对称点为A1,证明A1,D,B三点共线.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)过点E(0,-4)的直线与轨迹W交于两点A,B,点D是点E关于x轴的对称点,点A关于y轴的对称点为A1,证明A1,D,B三点共线.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由动点P(x,y)到F(0,1)的距离比到直线y=-2的距离小1,可得动点P(x,y)到F(0,1)的距离等于它到直线y=-1的距离,利用抛物线的定义,即可求动点P的轨迹W的方程;
(Ⅱ)设直线l的方程为y=kx-4,代入抛物线方程,求出直线A1B的方程,证明直线A1B过点D(0,4),可证A1,D,B三点共线.
(Ⅱ)设直线l的方程为y=kx-4,代入抛物线方程,求出直线A1B的方程,证明直线A1B过点D(0,4),可证A1,D,B三点共线.
解答:
(Ⅰ)解:∵动点P(x,y)到F(0,1)的距离比到直线y=-2的距离小1,
∴动点P(x,y)到F(0,1)的距离等于它到直线y=-1的距离,
∴动点P的轨迹W是以F(0,1)为焦点的抛物线,其方程为x2=4y;
(Ⅱ)证明:设直线l的方程为y=kx-4,A(x1,y1),B(x2,y2),则A1(-x1,y1),
由
消去y可得x2-4kx+16=0,
则△=16k2-64>0,即|k|>2,
x1+x2=4k,x1x2=16.
直线A1B:y-y2=
(x-x2),
∴y=
(x-x2)+
x22,
∴y=
x+
,
∴y=
x+4,
∴直线A1B过点D(0,4),
∴A1,D,B三点共线.
∴动点P(x,y)到F(0,1)的距离等于它到直线y=-1的距离,
∴动点P的轨迹W是以F(0,1)为焦点的抛物线,其方程为x2=4y;
(Ⅱ)证明:设直线l的方程为y=kx-4,A(x1,y1),B(x2,y2),则A1(-x1,y1),
由
|
则△=16k2-64>0,即|k|>2,
x1+x2=4k,x1x2=16.
直线A1B:y-y2=
| y2-y1 |
| x2+x1 |
∴y=
| x22-x12 |
| 4(x1+x2) |
| 1 |
| 4 |
∴y=
| x2-x1 |
| 4 |
| x1x2 |
| 4 |
∴y=
| x2-x1 |
| 4 |
∴直线A1B过点D(0,4),
∴A1,D,B三点共线.
点评:本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查学生的计算能力,确定直线A1B的方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={1,2},B={1,a,b},则“a=2”是“A⊆B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
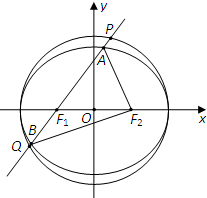 已知椭圆
已知椭圆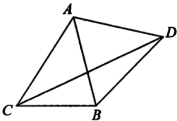 如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.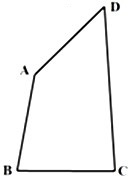 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=