Question

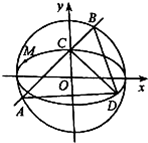已知椭圆C₁：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

3

2

，且经过点M(-

3

，

1

2

)，圆C2的直径C₁的长轴．如图，C是椭圆短轴端点，动直线AB过点C且与圆C₂交于A，B两点，CD垂直于AB交椭圆于点D．
（Ⅰ）求椭圆C₁的方程；
（Ⅱ）求△ABD面积的最大值，并求此时直线AB的方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知条件得

c

a

=

3

2

，所以设椭圆方程为

x2

4k2

+

y2

k2

=1，再由椭圆C₁经过点M(-

3

，

1

2

)，圆C2

3

，

1

2

），能求出椭圆C₁的方程．
（2）设A（x₁，y₁），B（x₂，y₂），D（x₀，y₀），设直线l₁的方程为y=kx+1，又圆C₂：x²+y²=4，求出点O到直线l₁的距离和|AB|，求出直线l₂的方程为x+ky-k=0．由此能求出直线l₁的方程．

解答： 解：（1）∵椭圆C₁：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

3

2

，
∴

c

a

=

3

2

，∴a=2k，b=k，k＞0，
∴

x2

4k2

+

y2

k2

=1，
∵椭圆C₁经过点M(-

3

，

1

2

)，圆C2

3

，

1

2

），
∴

3

4k2

+

1

4k2

=1，解得k²=1，
∴椭圆C₁的方程为

x2

4

+y2=1．
（2）设A（x₁，y₁），B（x₂，y₂），D（x₀，y₀），
由题意知直线l₁的斜率存在，设直线l₁的方程为y=kx+1，
又圆C₂：x²+y²=4，
∴点O到直线l₁的距离d=

1

k2+1

，
∴|AB|=2

4-d2

=2

4k2+3 k2+1

，
又∵l₁⊥l₂，∴直线l₂的方程为x+ky-k=0．
由

x+ky-k=0 x2 4 +y2=1

，消去y，得：
（4+k²）x²+8kx=0，
∴x0=-

8k

4+k2

，
∴|CD|=

8 k2+1

4+k2

，
设△ABD的面积为S，则S=

1

2

|AB|•|CD|=

8 4k2+3

4+k2

，
∴S=

32

4k2+3 + 13 4k2+3

≤

32

2 4k2+3 • 13 4k2+3

=

16 13

13

，
当且仅当k=±

10

2

时取等号，
∴所求的直线l₁的方程为y=±

10

2

x-1．

点评：本题考查椭圆的几何性质，考查直线与圆的位置关系，考查直线与椭圆的位置关系等基本知识，同时考查解析几何的解题思想和综合解题能力．