题目内容
4.集合$\left\{{x∈N|\frac{6}{x}∈N}\right\}$的真子集有( )个.| A. | 8 | B. | 16 | C. | 15 | D. | 14 |
分析 根据题意,求出集合$\left\{{x∈N|\frac{6}{x}∈N}\right\}$,再求它的真子集.
解答 解:集合$\left\{{x∈N|\frac{6}{x}∈N}\right\}$={1,2,3,6},
∴该集合的真子集有∅,{1},{2},{3},{6},{1,2},{1,3},{1,6},
{2,3},{2,6},{3,6},{1,2,3},{1,2,6},{2,3,6},{1,3,6}共15个.
故选:C.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设f(x)=lg$\frac{2+x}{2-x}$,则f(5x-3)的定义域为( )
| A. | (-$\frac{74}{25},22$) | B. | (-$\frac{74}{25},25$) | C. | (-2,2) | D. | (0,1) |
12.设变量x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥3x\\ x+ay≤7\end{array}\right.$,若目标函数z=x+y的最大值为14,则a值为( )
| A. | 1 | B. | $\frac{1}{2}$或$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
9.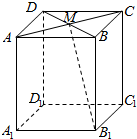 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
16. 某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )
某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )
 某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )
某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )| A. | $1+\sqrt{3}$ | B. | $1+2\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | 2$\sqrt{2}$ |
13.函数y=${3^{\sqrt{x}}}$的值域为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | [3,+∞) | D. | [9,+∞) |
14.点P(2,0)关于直线x+y+1=0对称点Q的坐标为( )
| A. | (-1,-3) | B. | (3,3) | C. | (-1,3) | D. | (4,-2) |