题目内容
如图，已知椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 4 |
| 3 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）探究
| OA |
| OB |
| OA |
| OB |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）把F2（c，0）代入
+
=1得y=
，从而可得|MF2|=
，|MF1|=
，由
+
=2a及a2-b2=c2=
2=2，可求a2，b2；
（2））①若直线l的斜率不存在时，易证：
•
=0；②若直线l的斜率存在时，设其方程为：y=kx+m，由直线与圆相切，得
=
，整理得3m2=4k2+4，联立y=kx+m与椭圆方程有（2k2+1）x2+4kmx+2m2-4=0，设A（x1，y1），B（x2，y2），由韦达定理及向量数量积运算可求结果；
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
| 3b2 |
| a |
| b2 |
| a |
| 3b2 |
| a |
| 2 |
（2））①若直线l的斜率不存在时，易证：
| OA |
| OB |
| |m| | ||
|
| 2 | ||
|
解答：
解：（1）把F2（c，0）代入
+
=1得y=
，
则|MF2|=
，由|MF1|：|MF2|=3：1得|MF1|=
，
又
+
=2a，∴a2=2b2，
∵a2-b2=c2=
2=2，
∴b2=2，a2=4，
∴
+
=1．
（2）①若直线l的斜率不存在时，易证：
•
=0，
②若直线l的斜率存在时，设其方程为：y=kx+m，直线与圆相切，
则
=
，从而3m2=4k2+4，
把直线方程：y=kx+m代入椭圆方程有（2k2+1）x2+4kmx+2m2-4=0，
设A（x1，y1），B（x2，y2），则△＞0，且x1+x2=
，x1x2=
，
•
=x1x2+y1y2=
(3m2-4k2-4)=0．
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
则|MF2|=
| b2 |
| a |
| 3b2 |
| a |
又
| b2 |
| a |
| 3b2 |
| a |
∵a2-b2=c2=
| 2 |
∴b2=2，a2=4，
∴
| x2 |
| 4 |
| y2 |
| 2 |
（2）①若直线l的斜率不存在时，易证：
| OA |
| OB |
②若直线l的斜率存在时，设其方程为：y=kx+m，直线与圆相切，
则
| |m| | ||
|
| 2 | ||
|
把直线方程：y=kx+m代入椭圆方程有（2k2+1）x2+4kmx+2m2-4=0，
设A（x1，y1），B（x2，y2），则△＞0，且x1+x2=
| -4km |
| 2k2+1 |
| 2m2-4 |
| 2k2+1 |
| OA |
| OB |
| 1 |
| 2k2+1 |
点评：该题考查椭圆的方程、性质，考查直线与椭圆的位置关系，考查方程思想，考查学生运算求解能力．
练习册系列答案
相关题目
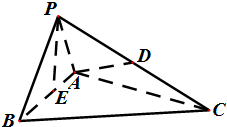如图，四面体P-ABC中，△PAB为边长为1的等边三角形，△PBC与△PAC均为斜边为PC的直角三角形，且PC=
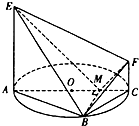如图，AC是圆O的直径，点B在圆O上，∠BAC=30°，BM⊥AC交AC于点M，EA⊥平面ABC，FC∥EA，AC=4，EA=3，FC=1．