题目内容
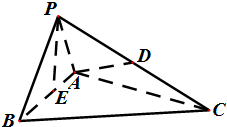 如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=
如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=| 3 |
(1)求证:PE与AC不垂直;
(2)求异面直线PB与AD所成角的大小.
考点:反证法与放缩法,异面直线及其所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)假设PE与AC垂直,证明AC⊥平面PAB,推出AC⊥AB,通过CA=CB,证明CE⊥AB,得到AC∥CE,推出矛盾,得到PE与AC不垂直.
(2)取BC的中点为F,联结DF、AF,说明∠ADF为异面直线PB与AD所成角(或其补角,在△ABC中,求解异面直线PB与AD所成角的大小即可.
(2)取BC的中点为F,联结DF、AF,说明∠ADF为异面直线PB与AD所成角(或其补角,在△ABC中,求解异面直线PB与AD所成角的大小即可.
解答:
 解:(1)假设PE与AC垂直,由已知可得:AC⊥PA,
解:(1)假设PE与AC垂直,由已知可得:AC⊥PA,
又因为PA与PE在平面PAB内交于点P,∴AC⊥平面PAB-------------2’
AB
平面PAB,∴AC⊥AB-------------------------------3’
又由已知可得:△PAC≌△PBC则可得:CA=CB--------------------4’
连结CE可得:CE⊥AB-----------------------------------5’
∴AC∥CE,显然与AC与CE相交矛盾,
∴PE与AC不垂直------------6’
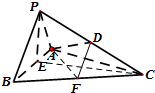
(2)取BC的中点为F,联结DF、AF,
∵D、F分别为PC、BC的中点,
∴DF∥PB,
∴∠ADF为异面直线PB与AD所成角(或其补角)------------------------------8’
在△ABC中,AC=BC=
=
,AB=1,可得:cosB=
--------9’
∴AF=
=1------------10’
在△ADF中,AD=
,DF=
,
∵AD2+DF2=AF2,∴∠ADF=90°------11’
∴异面直线PB与AD所成角的大小为90°--------------------------------------------12’
 解:(1)假设PE与AC垂直,由已知可得:AC⊥PA,
解:(1)假设PE与AC垂直,由已知可得:AC⊥PA,又因为PA与PE在平面PAB内交于点P,∴AC⊥平面PAB-------------2’
AB
|
又由已知可得:△PAC≌△PBC则可得:CA=CB--------------------4’
连结CE可得:CE⊥AB-----------------------------------5’
∴AC∥CE,显然与AC与CE相交矛盾,
∴PE与AC不垂直------------6’
(2)取BC的中点为F,联结DF、AF,
∵D、F分别为PC、BC的中点,
∴DF∥PB,
∴∠ADF为异面直线PB与AD所成角(或其补角)------------------------------8’
在△ABC中,AC=BC=
| 3-1 |
| 2 |
| ||
| 4 |
∴AF=
1+
|
在△ADF中,AD=
| ||
| 2 |
| 1 |
| 2 |
∵AD2+DF2=AF2,∴∠ADF=90°------11’
∴异面直线PB与AD所成角的大小为90°--------------------------------------------12’
点评:本题考查利用反证法证明直线与直线不垂直,异面直线所成角是求法,考查空间想象能力,逻辑推理能力和计算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
二项式(2
-
)5的展开式中含
项的系数为( )
| x |
| 1 |
| x |
| 1 |
| x2 |
| A、10 | B、-10 |
| C、40 | D、-40 |
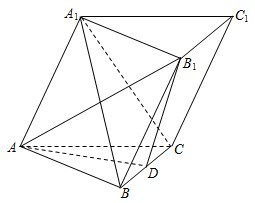 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点.
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点. 如图,已知椭圆E:
如图,已知椭圆E: