题目内容

已知
m
=（sinθ，1），
n
=（2cosθ，1），
m
∥
n
，求tan（
π
4
+2θ）．
考点：两角和与差的正切函数,平面向量共线（平行）的坐标表示
专题：三角函数的图像与性质
分析：通过向量平移，推出sinθ，cosθ的关系，然后求解tan（
π
4
+2θ）．
解答： 解：∵
m
=（sinθ，1），
n
=（2cosθ，1），
m
∥
n
，
∴sinθ=2cosθ，
∴tanθ=2．
tan2θ=
2tanθ
1-tan2θ
=-
4
3
．
∴tan（
π
4
+2θ）=
1+tan2θ
1-tan2θ
=
1-
4
3
1+
4
3
=-
1
7
．
点评：本题考查三角函数的化简求值，两角和与差的三角函数的应用，考查计算能力．
练习册系列答案
相关题目
某种零件按质量标准分为1，2，3，4，5五个等级，现从-批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下：
等级 1 2 3 4 5
频率 0.05 m 0.15 0.35 n
（1）在抽取的20个零件中，等级为5的恰有2个，求m，n的值；
（2）在（1）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级不相同的概率．
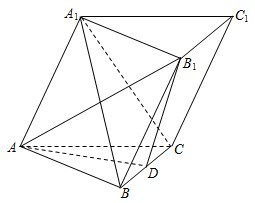在斜三棱柱ABC-A1B1C1中，侧面ACC1A1⊥平面ABC，∠ACB=90°，D为BC中点．
（Ⅰ）求证：BC⊥AA1；
（Ⅱ）求证：A1C∥平面AB1D；
（Ⅲ）若AC=AA1=BC=2，∠A1AC=60°，求三棱锥A1-ABC的体积．
如图，已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2且焦距为2
2
．点M为椭圆E上的一个动点，当MF2垂直于x轴时，恰好|MF1|：|MF2|=3：1．已知直线l与圆C：x2+y2=
4
3
相切，且与椭圆E相交于A、B两点，O为坐标原点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）探究
OA
•
OB
是否为定值，若是，求出
OA
•
OB
的值；若不是，请说明理由．
设数列{an}的前n项和为Sn，a1=1，an=
Sn
n
+n-1．
（1）求证：数列{an}为等差数列，并写出an与Sn的关于n的表达式；
（2）设数列{
1
anan+1
}的前n项和为Tn，证明：
1
3
≤Tn＜
1
2
；
（3）是否存在自然数n，使得2S1+
2S2
2
+
2Sn
n
-（n-2）2=2011．
求多项式﹙x-1﹚-﹙x-1﹚2+﹙x-1﹚3-﹙x-1﹚4+﹙x-1﹚5的展开式中的x3的系数．
设函数f（x）=ax2-2lnx
（1）讨论函数f（x）的单调区间；
（2）若函数g（x）=x2-2bx+4，当a=1时，若对任意x1∈（
1
2
，
3
2
），当任意x2∈[2，4]时，f（x1）≥g（x2）恒成立，求实数b的取值范围．
设函数f（x）=|x-a|
（Ⅰ）当a=2，解不等式f（x）≥4-|x-1|；
（Ⅱ）若f（x）≤1的解集为{x|0≤x≤2}，
1
m
+
1
2n
=a（m＞0，n＞0）．求证：m+2n≥4．
设a=
2
，b=
5
-
2
，c=
6
-
3
，则a，b，c从小到大的排列顺序是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网