题目内容
全美职业篮球联赛(NBA)某年度总决赛在雷霆队与迈阿密热火队之间角逐,比赛采用七局四胜制,即若有一队先胜四场,则此队获胜,比赛就此结束.因两队实力相当,故每场比赛获胜的可能性相等.据以往资料统计,第一场比赛组织者可获门票收入2000万美元,以后每场比赛门票收入比上场增加100万美元,当两队决出胜负后,问:
(1)组织者在此次决赛中要获得门票收入不少于13500万元的概率为多少?
(2)某队在比赛过程中曾一度比分落后2分以上,最后取得全场胜利称为“逆袭”,求雷霆队“逆袭”获胜的概率;
(3)求此次决赛所需比赛场数的分布列及数学期望.
(1)组织者在此次决赛中要获得门票收入不少于13500万元的概率为多少?
(2)某队在比赛过程中曾一度比分落后2分以上,最后取得全场胜利称为“逆袭”,求雷霆队“逆袭”获胜的概率;
(3)求此次决赛所需比赛场数的分布列及数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(1)先确定至少要比赛6场,再求出相应的概率,即可求出组织者在此次决赛中要获得门票收入不少于13500万元的概率为多少?
(2)雷霆队“逆袭”获胜,可能通过6场或7场获胜,分类求概率,即可求雷霆队“逆袭”获胜的概率;
(3)所需比赛场数ξ是随机变量,其取值为4,5,6,7.求出相应的概率,即可求此次决赛所需比赛场数的分布列及数学期望.
(2)雷霆队“逆袭”获胜,可能通过6场或7场获胜,分类求概率,即可求雷霆队“逆袭”获胜的概率;
(3)所需比赛场数ξ是随机变量,其取值为4,5,6,7.求出相应的概率,即可求此次决赛所需比赛场数的分布列及数学期望.
解答:
解:(1)因2000+2100+2200+2300+2400+2500=13500,故至少要比赛6场.
当进行比赛6场时,某一队获胜的概率为P(6)=
,
当进行比赛7场时,某一队获胜的概率为P(7)=
,
所以收入不少于13500万元的概率为P(6)+P(7)=
+
=
=0.625.
(2)雷霆队“逆袭”获胜,可能通过6场或7场获胜.
当6场获胜时,则1、2场败,3、4、5、6胜,概率为(
)6=
;
当7场获胜时,则4胜3败,
①若前2场都败,则另外1败可以任意发生在第3、4、5、6中的一场,所以“逆袭”获胜概率为
•(
)7=
.②若前2场1胜1败,则第3、4场必须败,所以“逆袭”获胜概率为
•(
)7=
,
故雷霆队“逆袭”获胜的概率为
+
+
=
.
(3)所需比赛场数ξ是随机变量,其取值为4,5,6,7.若比赛最终获胜队在第k场获胜后结束比赛,则显然在前面k-1场中获胜3场,
从而P(ξ=k)=
(
)k-1,k=4,5,6,7.
①分布列为:
②所需比赛场数的数学期望是E(ξ)=4×
+5×
+6×
+7×
=
.
当进行比赛6场时,某一队获胜的概率为P(6)=
| 5 |
| 16 |
当进行比赛7场时,某一队获胜的概率为P(7)=
| 5 |
| 16 |
所以收入不少于13500万元的概率为P(6)+P(7)=
| 5 |
| 16 |
| 5 |
| 16 |
| 5 |
| 8 |
(2)雷霆队“逆袭”获胜,可能通过6场或7场获胜.
当6场获胜时,则1、2场败,3、4、5、6胜,概率为(
| 1 |
| 2 |
| 1 |
| 64 |
当7场获胜时,则4胜3败,
①若前2场都败,则另外1败可以任意发生在第3、4、5、6中的一场,所以“逆袭”获胜概率为
| C | 1 4 |
| 1 |
| 2 |
| 1 |
| 32 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 64 |
故雷霆队“逆袭”获胜的概率为
| 1 |
| 64 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 16 |
(3)所需比赛场数ξ是随机变量,其取值为4,5,6,7.若比赛最终获胜队在第k场获胜后结束比赛,则显然在前面k-1场中获胜3场,
从而P(ξ=k)=
| C | 3 k-1 |
| 1 |
| 2 |
①分布列为:
| ξ | 4 | 5 | 6 | 7 | ||||||||
| P |
|
|
|
|
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 93 |
| 16 |
点评:本题考查概率的计算,考查离散型随机变量的分布列和期望,考查分类讨论的数学思想,正确求概率是关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
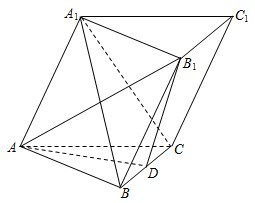 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点.
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°,D为BC中点. 如图,已知椭圆E:
如图,已知椭圆E: 如图,设A、B、C、D为球O上的四点,若AD⊥平面ABC,且AD=2,∠BAC=60°,AB=2
如图,设A、B、C、D为球O上的四点,若AD⊥平面ABC,且AD=2,∠BAC=60°,AB=2