题目内容
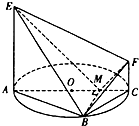 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(Ⅰ)证明:AB⊥BF;
(Ⅱ)求三棱锥E-BMF的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:计算题,证明题
分析:(Ⅰ)证明AB⊥BF,转化成证明线面垂直,即证AB⊥平面BFC;
(Ⅱ)求三棱锥E-BMF的体积,转化成求三棱锥B-EMF的体积.
(Ⅱ)求三棱锥E-BMF的体积,转化成求三棱锥B-EMF的体积.
解答:
解:(Ⅰ)证明:∵EA⊥平面ABC,FC∥EA,
∴FC⊥平面ABC
∵AB?平面ABC
∴FC⊥AB
又∵AC是直径,B在圆上,
∴AB⊥BC
∴AB⊥平面BFC
又∵BF?平面BFC
∴AB⊥BF.
(Ⅱ)在△ABC中,∠BAC=30°,BM⊥AC交AC于点M,AC=4,
∴BM=
,
三角形EMF的面积S=
(3+1)×4-
×3×3-
×1×1=3
VE-BMF=VB-EMF=
×3×
=
.
∴FC⊥平面ABC
∵AB?平面ABC
∴FC⊥AB
又∵AC是直径,B在圆上,
∴AB⊥BC
∴AB⊥平面BFC
又∵BF?平面BFC
∴AB⊥BF.
(Ⅱ)在△ABC中,∠BAC=30°,BM⊥AC交AC于点M,AC=4,
∴BM=
| 3 |
三角形EMF的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
VE-BMF=VB-EMF=
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查了线面位置关系的证明及几何体的体积,证明线线垂直可以转化成证明线面垂直;求三棱锥的体积关键是通过转换顶点转化成易求底面积和高的三棱锥的体积问题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
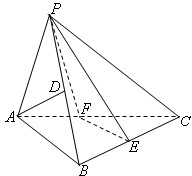 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点. 如图,已知椭圆E:
如图,已知椭圆E: