题目内容
如图1在等腰梯形B中,AB∥CD,AB=2BC=2CD=2,E是AB的中点,F是DE的中点,沿直线DE将△ADE翻折,使二面角A-DE-B为60°(如图2).
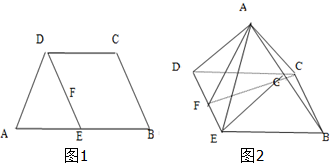
(Ⅰ)证明:FC不可能与AB垂直;
(Ⅱ)取AB的中点G,求证:EG∥面AFC;
(Ⅲ)求AB与面BCDE所成角的正切值.

(Ⅰ)证明:FC不可能与AB垂直;
(Ⅱ)取AB的中点G,求证:EG∥面AFC;
(Ⅲ)求AB与面BCDE所成角的正切值.
考点:直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)假设FC⊥AB,推出FC与AC成60°,说明假设不成立,即可证明:FC不可能与AB垂直;
(Ⅱ)取AB的中点G,取AC中点H,连FH,GH,利用直线与平面平行的判定定理证明EG∥面AFC;
(Ⅲ)取FC中点M,说明∠ABM为AB与面BCDE所成角.在△ABM中,求AB与面BCDE所成角的正切值.
(Ⅱ)取AB的中点G,取AC中点H,连FH,GH,利用直线与平面平行的判定定理证明EG∥面AFC;
(Ⅲ)取FC中点M,说明∠ABM为AB与面BCDE所成角.在△ABM中,求AB与面BCDE所成角的正切值.
解答:
解:(Ⅰ)证:假设FC⊥AB,由已知平面图形得FC⊥AB,
∴FC⊥面ACB,
∴FC⊥AC
由已知得∠AFC为A-DE-B的平面角60°,
又AF=FC∴△AFC为正三角形,
即FC与AC成60°∴假设不成立.
∴FC不可能与AB垂直.----------------------------------(5分)
(Ⅱ)取AC中点H,连FH,GH,
∴GH∥FE∥BC且GH=FE=
BC
即四边形EFHG为平行四边形∴FH∥EG,EG?面AFC,FH?面AFC,
∴EG∥面AFC------------------------------------------------(10分)
(Ⅲ)由已知得面AFC⊥面BCDE,取FC中点M,
得到AM⊥FC∴AM⊥面BCDE,
∴∠ABM为AB与面BCDE所成角.
记BC=a,则FC=
,
在△ABM中,
∴AM=
,BM=
∴tan∠ABM=
-------(15分)
∴FC⊥面ACB,
∴FC⊥AC
由已知得∠AFC为A-DE-B的平面角60°,
又AF=FC∴△AFC为正三角形,
即FC与AC成60°∴假设不成立.
∴FC不可能与AB垂直.----------------------------------(5分)
(Ⅱ)取AC中点H,连FH,GH,
∴GH∥FE∥BC且GH=FE=
| 1 |
| 2 |
即四边形EFHG为平行四边形∴FH∥EG,EG?面AFC,FH?面AFC,
∴EG∥面AFC------------------------------------------------(10分)
(Ⅲ)由已知得面AFC⊥面BCDE,取FC中点M,
得到AM⊥FC∴AM⊥面BCDE,
∴∠ABM为AB与面BCDE所成角.
记BC=a,则FC=
| ||
| 2 |
在△ABM中,
∴AM=
| 3a |
| 4 |
| ||
| 4 |
∴tan∠ABM=
3
| ||
| 19 |
点评:本题主要考查空间点、线、面位置关系,线面所成角等基础知识,同时考查空间想象能力和推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
二项式(2
-
)5的展开式中含
项的系数为( )
| x |
| 1 |
| x |
| 1 |
| x2 |
| A、10 | B、-10 |
| C、40 | D、-40 |
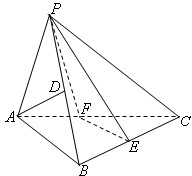 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点. 如图,已知椭圆E:
如图,已知椭圆E: