题目内容
19.在△ABC中,A=$\frac{π}{4}$,b2sin C=4$\sqrt{2}$sin B,则△ABC的面积为( )| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
分析 利用正弦定理求出bc的值,然后利用三角形的面积公式求解即可.
解答 解:在△ABC中,A=$\frac{π}{4}$,b2sin C=4$\sqrt{2}$sin B,
可得bc=4$\sqrt{2}$,
所以三角形的面积为:$\frac{1}{2}bcsinA$=$\frac{1}{2}×4\sqrt{2}×\frac{\sqrt{2}}{2}$=2.
故选:C.
点评 本题考查正弦定理的应用,三角形的面积的求法,考查计算能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
9.若复数z满足(1+i)z=|$\sqrt{3}$+i|,则在复平面内,z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.某区实验幼儿园对儿童记忆能力x与识图能力y进行统计分析,得到如下数据:
由表中数据,求得线性回归方程为$y=\frac{4}{5}x+a$,当江小豆同学的记忆能力为12时,预测他的识图能力为( )
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 9 | B. | 9.5 | C. | 10 | D. | 11.5 |
4. 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )| A. | 丙在Ⅲ区域,丁在Ⅰ区域 | B. | 丙在Ⅰ区城,丁在Ⅲ区域 | ||
| C. | 丙在Ⅱ区域,丁在Ⅰ区域 | D. | 丙在Ⅲ区域,丁在Ⅱ区域 |
11.命题“?x∈N,x≥0”的否定是( )
| A. | ?x∈N,x<0 | B. | ?x∉N,x≥0 | C. | ?x∈N,x<0 | D. | ?x∈N,x>0 |
8.已知$\frac{π}{2}<A<π$,且sinA=$\frac{4}{5}$,那么sin2A等于( )
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
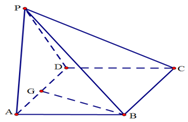 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.