题目内容

7．已知圆C的半径为2，圆心在x轴的正半轴上，直线3x+4y+4=0与圆C相切，则圆C的方程为（　　）
A．（x-1）2+y2=4B．（x-2）2+y2=4C．（x+1）2+y2=4D．（x+2）2+y2=4

分析 设出圆心坐标为C（a，0）（a＞0），由点到直线的距离公式列式求得a值，代入圆的标准方程得答案．

解答 解：设圆心坐标为C（a，0）（a＞0），
由题意得，$\frac{|3a+4×0+4|}{\sqrt{{3}^{2}+{4}^{2}}}=2$，解得a=2．
∴圆C的方程为（x-2）2+y2=4．
故选：B．

点评 本题考查圆的标准方程，考查了点到直线距离公式的应用，是基础题．

练习册系列答案
相关题目
17．一个总体中的80个个体编号为0，1，2，…，79，并依次将其分为8个组，组号为0，1，…，9，要用（错位）系统抽样的方法抽取一个容量为8的样本，即规定先在第1组随机抽取一个号码，记为i，依次错位地得到后面各组的号码，即第k组中抽取个位数为i+k（当i+k＜10）或i+k-10（当i+k≥10）的号码，在i=6时，所抽到的第8组的号码是74．
18．某企业有甲、乙两个研发小组，他们研发一件新产品成功的概率分别为$\frac{3}{4}$和$\frac{2}{3}$，本年度计划研发的新产品件数分别为2件和1件．设甲、乙两组的每次研发均相互独立．
（1）求该企业本年度至少有一件新产品研发成功的概率；
（2）已知研发一件新产品的成本为10百万元，成功研发一件新产品可获得50百万元的销售额，求该企业本年度在这3件新产品上获得的利润X的分布列和数学期望．
15．已知角α的终边经过点P（-1，1），则cosα的值为（　　）
A．1B．-1C．-$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{2}}{2}$
2．在△ABC中，角A，B，C所对的边分别为a，b，c，且b2+c2=a2+bc．
（1）求角A的大小；
（2）若三角形的面积为$\sqrt{3}$，且b+c=5，求b和c的值．
2．已知点P（3，1）在矩阵A=$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ 变换下得到点P′（5，-1）．试求矩阵A和它的逆矩阵A-1．
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，若圆x2+y2=a2被直线x-y-$\sqrt{2}$=0截得的弦长为2
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点A、B为动直线y=k（x-1），k≠0与椭圆C的两个交点，问：在x轴上是否存在定点M，使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值？若存在，试求出点M的坐标和定值；若不存在，请说明理由．
6．在极坐标系中，圆心在（$\sqrt{2}$，π）且过极点的圆的方程为（　　）
A．ρ=2$\sqrt{2}$cos θB．ρ=-2$\sqrt{2}$cos θC．ρ=2$\sqrt{2}$sin θD．ρ=-2$\sqrt{2}$sin θ
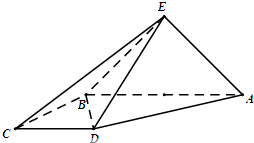7．如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直．AB∥CD，AB⊥BC，AB=2CD=2BC=2，EA⊥EB．
（1）求证：AB⊥DE；
（2）求直线EC与平面ABE所成角的正弦值；
（3）线段EA上是否存在点F，使EC∥平面FBD？若存在，求出$\frac{EF}{EA}$；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网