题目内容
17.一个总体中的80个个体编号为0,1,2,…,79,并依次将其分为8个组,组号为0,1,…,9,要用(错位)系统抽样的方法抽取一个容量为8的样本,即规定先在第1组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码,在i=6时,所抽到的第8组的号码是74.分析 求出样本间隔,结合条件,求出第8组中抽取个位数即可.
解答 解:由题意,样本间隔为80÷8=10,
则第8组抽取的号码在(70,79)之间,
若i=6,k=8时,6+8-10=4,则第8组抽取的号码为74,
故答案为74.
点评 本题考查了系统抽样方法,解答的关键是对题目给出的系统抽样的定义的理解,是基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.若函数y=f(x)是定义在R上的奇函数,且在区间(-∞,0]上是减函数,则不等式f(lnx)<-f(1)的解集为( )
| A. | (e,+∞) | B. | (${\frac{1}{e}$,+∞) | C. | (${\frac{1}{e}$,e) | D. | (0,$\frac{1}{e}$) |
7.已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x+1)2+y2=4 | D. | (x+2)2+y2=4 |
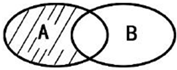 已知不等式|x-2|<3的解集为 A,函数y=ln(1-x)的定义域为B,则图中阴影部分表示的集合为{x|1≤x<5}.
已知不等式|x-2|<3的解集为 A,函数y=ln(1-x)的定义域为B,则图中阴影部分表示的集合为{x|1≤x<5}.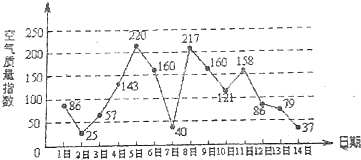 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.