题目内容
2.已知点P(3,1)在矩阵A=$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ 变换下得到点P′(5,-1).试求矩阵A和它的逆矩阵A-1.分析 由$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ $[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{3a+2}\\{2b-1}\end{array}]$=$[\begin{array}{l}{5}\\{-1}\end{array}]$,列方程求得a和b的值,求得矩阵A,丨A丨及A*,由A-1=$\frac{1}{丨A丨}$•A*,即可求得A-1.
解答 解:依题意得$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ $[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{3a+2}\\{2b-1}\end{array}]$=$[\begin{array}{l}{5}\\{-1}\end{array}]$,
所以$\left\{\begin{array}{l}3a+2=5\\ 3b-1=-1\end{array}$,解得:$\left\{\begin{array}{l}a=1\\ b=0\end{array}$,
A=$[\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}]$,
丨A丨=$|\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}|$=1×(-1)-0×2=-1,
A*=$[\begin{array}{l}{-1}&{-2}\\{0}&{1}\end{array}]$,
∴A-1=$\frac{1}{丨A丨}$•A*=$[\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}]$,
∴A-1=$[\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}]$.
点评 本题考查矩阵的变换,逆矩阵的求法,考查计算能力,属于基础题.

| A. | (e,+∞) | B. | (${\frac{1}{e}$,+∞) | C. | (${\frac{1}{e}$,e) | D. | (0,$\frac{1}{e}$) |
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x+1)2+y2=4 | D. | (x+2)2+y2=4 |
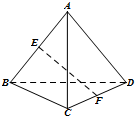 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | ρsinθ=3 | B. | ρcosθ=3 | C. | $ρ=6sin(θ+\frac{π}{3})$ | D. | $ρ=6sin(θ-\frac{π}{3})$ |