题目内容
2.在△ABC中,角A,B,C所对的边分别为a,b,c,且b2+c2=a2+bc.(1)求角A的大小;
(2)若三角形的面积为$\sqrt{3}$,且b+c=5,求b和c的值.
分析 (1)由b2+c2=a2+bc,利用余弦定理可得cosA=$\frac{1}{2}$,即可得出.
(2)S△ABC=$\frac{1}{2}bc$sin$\frac{π}{3}$=$\sqrt{3}$,化为:bc=4,又b+c=5,联立解出b,c.
解答 解:(1)∵b2+c2=a2+bc,∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),∴A=$\frac{π}{3}$.
(2)S△ABC=$\frac{1}{2}bc$sin$\frac{π}{3}$=$\sqrt{3}$,化为bc=4,
又b+c=5,解得b=4,c=1或b=1,c=4.
点评 本题考查了余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.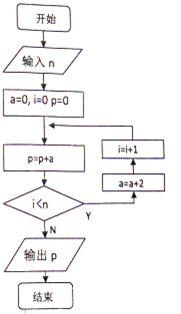 执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
 执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )| A. | 12 | B. | 42 | C. | 30 | D. | 40 |
17.若函数f(x)=(x-2)(x+a)是偶函数,则实数a的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
7.已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x+1)2+y2=4 | D. | (x+2)2+y2=4 |
1.设随机变量X~B ( n,p ),且EX=6,DX=3,则P(X=1)的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |
2.图(1)、图(2)、图(3)、图(4)分别包含1、5、13和25个互不重叠的单位正方形,按同样的方式构造图形,则第n个图包含( )个互不重叠的单位正方形.
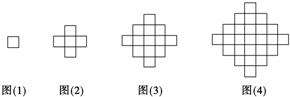

| A. | n2-2n+1 | B. | 2n2-2n+1 | C. | 2n2+2 | D. | 2n2-n+1 |