题目内容
9.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,若圆x2+y2=a2被直线x-y-$\sqrt{2}$=0截得的弦长为2(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点A、B为动直线y=k(x-1),k≠0与椭圆C的两个交点,问:在x轴上是否存在定点M,使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
分析 (I)求出圆x2+y2=a2的圆心(0,0)到直线x-y-$\sqrt{2}$=0的距离d,利用2=2$\sqrt{{a}^{2}-{d}^{2}}$,解得a2,又$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2=b2+c2,联立解出即可得出.
(II)假设在x轴上存在定点M(m,0),使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值.设A(x1,y1),B(x2,y2),直线方程与椭圆方程联立化为:(1+2k2)x2-4k2x+2k2-2=0,
利用根与系数的关系及其数量积运算性质可得$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{{k}^{2}(2{m}^{2}-4m+1)+{m}^{2}-2}{2{k}^{2}+1}$,令2m2-4m+1=2(m2-2),解得m即可得出.
解答 解:(I)圆x2+y2=a2的圆心(0,0)到直线x-y-$\sqrt{2}$=0的距离d=$\frac{|0-\sqrt{2}|}{\sqrt{2}}$=1,
∴2=2$\sqrt{{a}^{2}-{1}^{2}}$,解得a2=2,又$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2=b2+c2,
联立解得:a2=2,c=1=b.
∴椭圆C的标准方程为:$\frac{{x}^{2}}{2}$+y2=1.
(II)假设在x轴上存在定点M(m,0),使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值.
设A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为:(1+2k2)x2-4k2x+2k2-2=0,
则x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1•x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$.
$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1-m,y1)•(x2-m,y2)=(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1-1)(x2-1)=(1+k2)x1•x2-(m+k2)(x1+x2)+m2+k2
=(1+k2)•$\frac{2{k}^{2}-2}{1+2{k}^{2}}$-(m+k2)$\frac{4{k}^{2}}{1+2{k}^{2}}$+m2+k2
=$\frac{{k}^{2}(2{m}^{2}-4m+1)+{m}^{2}-2}{2{k}^{2}+1}$,
令2m2-4m+1=2(m2-2),解得m=$\frac{5}{4}$.
因此在x轴上存在定点M($\frac{5}{4}$,0),使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值$-\frac{7}{16}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质、定值,考查了推理能力与计算能力,属于难题.

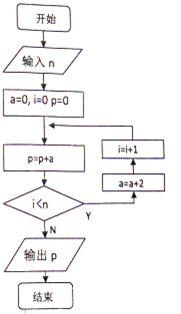 执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )| A. | 12 | B. | 42 | C. | 30 | D. | 40 |
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x+1)2+y2=4 | D. | (x+2)2+y2=4 |
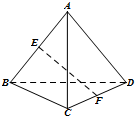 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |