题目内容
(1)已知tanα=2,求sin2α-3sinαcosα+1的值;
(2)求函数y=cos2x+sinx的值域.
(2)求函数y=cos2x+sinx的值域.
考点:三角函数的最值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)由条件利用同角三角函数的基本关系,把要求的式子化为
,再把tanα=2代入运算可得结果.
(2)利用二倍角的余弦公式化简函数的解析式为y=-2(sinx-
)2+
,结合正弦函数的值域,利用二次函数的性质求得函数y的最值,可得函数的值域.
| 2tan2α-3tanα+1 |
| tan2α+1 |
(2)利用二倍角的余弦公式化简函数的解析式为y=-2(sinx-
| 1 |
| 4 |
| 9 |
| 8 |
解答:
解:(1)∵tanα=2,
∴sin2α-3sinαcosα+1=2sin2α-3sinαcosα+cos2α
=
=
=
=
.
(2)函数y=cos2x+sinx=1-2sin2x+sinx=-2(sinx-
)2+
,
故当sinx=
时,函数取得最大值为
,当sinx=-1时,函数取得最小值为-2,
故函数的值域为[-2,
].
∴sin2α-3sinαcosα+1=2sin2α-3sinαcosα+cos2α
=
| 2sin2α-3sinαcosα+cos2α |
| sin2α+cos2α |
| 2tan2α-3tanα+1 |
| tan2α+1 |
| 2×4-3×2+1 |
| 4+1 |
| 3 |
| 5 |
(2)函数y=cos2x+sinx=1-2sin2x+sinx=-2(sinx-
| 1 |
| 4 |
| 9 |
| 8 |
故当sinx=
| 1 |
| 4 |
| 9 |
| 8 |
故函数的值域为[-2,
| 9 |
| 8 |
点评:本题主要考查同角三角函数的基本关系,正弦函数的值域,二倍角的余弦公式,二次函数的性质的应用,属于基础题.

练习册系列答案
相关题目
若函数f(x)=2sin(2x+
),则它的图象的一个对称中心为( )
| π |
| 4 |
A、(-
| ||
B、(
| ||
| C、(0,0) | ||
D、(-
|
“a=2”是“直线2x+ay+2=0与直线ax+2y-2=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=
为R的单调函数,则实数a的取值范围是( )
|
| A、(0,+∞) |
| B、[-1,0) |
| C、(-2,0) |
| D、(-∞,-2) |
长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于( )
| A、30° | B、45° |
| C、60° | D、90° |
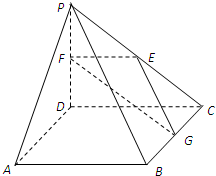 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.