题目内容
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、±
| ||||
D、y=±
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线的离心率求出c与a的关系,再根据a、b、c的关系求出
的值即得渐近线的方程.
| a |
| b |
解答:
解:∵双曲线
-
=1(a>0,b>0)的离心率为
,
即
=
,
∴c=
a;
又∵c2=a2+b2,
∴
a2=a2+b2,
∴
a2=b2,
∴
=
;
∴双曲线的渐近线方程为y=±
x.
故选:B.
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
即
| c |
| a |
| ||
| 2 |
∴c=
| ||
| 2 |
又∵c2=a2+b2,
∴
| 6 |
| 4 |
∴
| 1 |
| 2 |
∴
| a |
| b |
| 2 |
∴双曲线的渐近线方程为y=±
| 2 |
故选:B.
点评:本题考查了双曲线的几何性质的应用问题,解题时应灵活利用双曲线的离心率、a、b、c的关系以及渐近线的方程,是基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
已知A、B是抛物线y2=4p上不同的两点,且直线AB的倾斜角为锐角,F为抛物线的焦点,且
=-4
,则直线AB的斜率为( )
| FA |
| FB |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.
如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.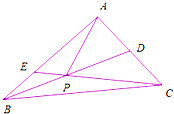 如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若
如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若