题目内容
函数y=
，x∈[0，+∞）的值域为（ ）
| x-1 |
| x+1 |
| A、[-1，1） |
| B、（-1，1] |
| C、[-1，+∞） |
| D、[0，+∞） |
考点：函数的值域
专题：函数的性质及应用
分析：本题可将原函数转化为部分分式的形式，然后根据函数的定义域，求出相应代数式的取值范围，得到本题结论．
解答：
解：∵x∈[0，+∞），
∴x+1≥1，
∴0＜
≤1，
∴-2≤
＜0，
∴-1≤1+
＜1，
∴函数y=
=1+
的值域为：[-1，1）．
故选A．
∴x+1≥1，
∴0＜
| 1 |
| x+1 |
∴-2≤
| -2 |
| x+1 |
∴-1≤1+
| -2 |
| x+1 |
∴函数y=
| x-1 |
| x+1 |
| -2 |
| x+1 |
故选A．
点评：本题考查了函数的值域，本题难度不大，属于基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知=
（1，2），
=（0，1），
=（-2，k），若（
+2
）⊥
，则k=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
如图所示，平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上，且直线EH与FG相交于点P，求证：B、D、P三点共线．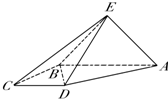
如图，四棱锥E-ABCD中，面ABE⊥面ABCD，侧面ABE是等腰直角三角形，EA⊥EB，且AB∥CD，AB⊥BC，AB=2CD=2BC=2．
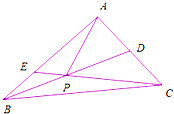如图三角形ABC中，AD=DC，AE=2EB，BD与CE相交于点P，若