题目内容
在△ABC中，a、b、c为角A、B、C的对边，如果∠A=35°，a=10，b=15，则此三角形有（ ）
| A、一解 | B、两解 |
| C、无解 | D、无穷多解 |
考点：正弦定理
专题：解三角形
分析：先应用正弦定理，求出sinB，并判断与1的大小，再根据三角形的边角关系，从而确定B的个数，即可判断三角形的个数．
解答：
解：∵∠A=35°，a=10，b=15，
∴由正弦定理得，
=
，
∴sinB=
sin35°＜1，
又∵a＜b，∴A＜B，
又A为锐角，∴B为锐角或为钝角，
∴三角形的个数为2．
故选B．
∴由正弦定理得，
| 10 |
| sin35° |
| 15 |
| sinB |
∴sinB=
| 3 |
| 2 |
又∵a＜b，∴A＜B，
又A为锐角，∴B为锐角或为钝角，
∴三角形的个数为2．
故选B．
点评：本题主要考查正弦定理以及应用，求解三角形的个数，应结合三角形的边角关系，以及正弦函数的值域，这是一道基础题．
练习册系列答案
全优点练单元计划系列答案
相关题目
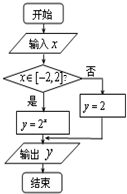
已知数列{an}中，a1=1，an+1=2an+n-1，若利用如图所示的程序框图进行运算，则输出n的值为阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
已知集合A=（-1，2），集合B={x|-x2-2x+3＞0}，则A∪B=（ ）
| A、（-1，1） |
| B、（-3，2） |
| C、（-1，3） |
| D、（-1，2） |
一个算法的程序框图如图所示，若执行该程序输出的结果为| 99 |
| 100 |
| A、i≤98？ |
| B、i≤99？ |
| C、i≤100？ |
| D、i≤101？ |
已知f（x）=ax和g（x）=bx是指数函数，则“f（2）＞g（2）”是“a＞b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
阅读如图程序框图，输出的结果s的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|