Question

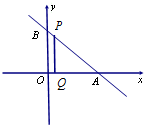如图直线l过点（3，4），与x轴、y轴的正半轴分别交于A、B两点，△ABC的面积为24．点P为线段AB上一动点，且PQ∥QB交OA于点Q．
（Ⅰ）求直线AB斜率的大小；
（Ⅱ）若S_△PAQ=

1

3

SOQPB时，请你确定P点在AB上的位置，并求出线段PQ的长；
（Ⅲ）在y轴上是否存在点M，使△MPQ为等腰直角三角形，若存在，求出点M的坐标； 若不存在，说明理由．

Answer 1

考点：直线的一般式方程与直线的垂直关系,三角形的形状判断,直线的斜率

专题：

分析：（Ⅰ）设直线l方程为y-4=k（x-3），易得A（3-

4

k

，0），B（0，4-3k），由三角形的面积公式可得k的方程，解方程可得；
（Ⅱ）可得直线l的方程4x+3y-24=0，B（0，8），由S_△PAQ=

1

3

SOQPB和PQ∥QB可得△PAQ与△ABO相似，可得

PQ

BO

=

1

2

进而可得的PQ=4，即P点在线段AB的中点的时候，S_△PAQ=

1

3

SOQPB；
（Ⅲ）设M（0，b），Q（a，0），则P（a，8-

4

3

a），由题意可知k_MP•k_MQ=-1且b=

1

2

（8-

4

3

a），解方程组可得答案．

解答： 解：（Ⅰ）当直线l斜率不存在时，易知不符合题意．
∴设直线l方程为y-4=k（x-3），
∵A、B是直线l与x轴、y轴的正半轴的交点，
∴A（3-

4

k

，0），B（0，4-3k），
∴S_△ABO=

1

2

（3-

4

k

）（4-3k）=24，解得k=-

4

3

（Ⅱ）解：由（1）知直线l的方程为：y-4=-

4

3

(x-3)即4x+3y-24=0，
可得此时B的坐标为（0，8），∵S_△PAQ=

1

3

SOQPB，
∴S_△PAQ=

1

4

S_△ABO，∴

S△PAQ

S△ABO

=

1

4

，
∵PQ∥QB，∴△PAQ与△ABO相似，
∴

PQ2

BO2

=

1

4

，∴

PQ

BO

=

1

2

，∴PQ=4
∴P点在线段AB的中点的时候，S_△PAQ=

1

3

SOQPB；
（Ⅲ）存在点M（0，

12

5

），理由如下：
设M（0，b），Q（a，0），则P（a，8-

4

3

a），
由题意可知k_MP•k_MQ=-1且b=

1

2

（8-

4

3

a），
解方程组可得a=b=

12

5

，故存在点M（0，

12

5

）满足题意．

点评：本题考查直线的一般式方程和垂直关系，涉及三角形的面积公式和相似问题，属中档题．