题目内容
设x~N(3,22),求P(2≤x<4),P(x≥3),P(|x|>2).
考点:正态分布曲线的特点及曲线所表示的意义
专题:概率与统计
分析:根据随机变量x~N(3,22),得
~N(0,1),由标准正态分布表,即可求得结论.
| x-3 |
| 2 |
解答:
解:∵x~N(3,22),∴
~N(0,1),
∴P(2≤x<4)=P(-
≤
≤
)=∅(
)-∅(-
)=0.6915-(1-0.6915)=0.383
P(x≥3)=P(
≥0)=1-∅(0)=
,
P(|x|>2)=P(x>2或x<-2)=P(
>-
或
<-
)=1-∅(-
)+∅(-
)=∅(
)+1-∅(
)=0.6915+1-0.9938=0.6977.
| x-3 |
| 2 |
∴P(2≤x<4)=P(-
| 1 |
| 2 |
| x-3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
P(x≥3)=P(
| x-3 |
| 2 |
| 1 |
| 2 |
P(|x|>2)=P(x>2或x<-2)=P(
| x-3 |
| 2 |
| 1 |
| 2 |
| x-3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查正态分布,正态曲线的特点,若一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似的服从正态分布.

练习册系列答案
相关题目
已知f(x)=ax3-
-2(a,b≠0),若f(-2)=2,则f(2)的值等于 ( )
| b |
| x |
| A、-2 | B、-4 | C、-6 | D、-10 |
在正方体ABCD-A1B1C1D1中,AB=2,E是棱CD的中点,则三棱锥A1-BB1E的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
方程
=|x+y+2|表示( )
| 2(x+1)2+2(y-1)2 |
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
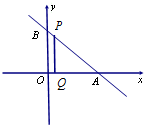 如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.