题目内容
函数y=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、{x|-1<x<1} |
| B、{x|x<-1,或x>1} |
| C、{x|0<x<1} |
| D、{-1,1} |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:要使函数有意义,则需1-x2≥0且x2-1≥0,解得即可得到定义域.
解答:
解:要使函数有意义,则需1-x2≥0且x2-1≥0,
解得x2≤1且x2≥1,则x2=1,即x=±1,
则定义域为{-1,1}.
故选D.
解得x2≤1且x2≥1,则x2=1,即x=±1,
则定义域为{-1,1}.
故选D.
点评:本题考查函数的定义域的求法,注意偶次根式被开方式非负,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了得到函数y=sin(2x-
)的图象,可以将函数y=cos2x的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知f(x)=ax3-
-2(a,b≠0),若f(-2)=2,则f(2)的值等于 ( )
| b |
| x |
| A、-2 | B、-4 | C、-6 | D、-10 |
函数f(x)=lgx-
的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
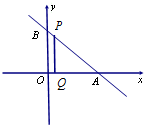 如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.