题目内容
把二进制数10110100化为十进制数为 ．
考点：进位制
专题：计算题
分析：本题考查的知识点是算法的概念，由二进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．
解答：
解：10110100（2）=1×22+1×24+1×25+1×27=180
故答案为：180．
故答案为：180．
点评：进制转换为十进制的方法是依次累加各位数字上的数×该数位的权重．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
已知a、b、c∈R，a＞b，则（ ）
| A、a+c＞b+c |
| B、a+c＜b+c |
| C、a+c≥b+c |
| D、a+c≤b+c |
函数f（x）=-x2+2（a-1）x+2在（-∞，2）上是增函数，则a的范围是（ ）
| A、a≥5 | B、a≥3 |
| C、a≤3 | D、a≤-5 |
为了得到函数y=sin（2x-
）的图象，可以将函数y=cos2x的图象（ ）
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
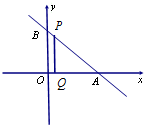如图直线l过点（3，4），与x轴、y轴的正半轴分别交于A、B两点，△ABC的面积为24．点P为线段AB上一动点，且PQ∥QB交OA于点Q．