题目内容
已知椭圆E:
+
=1(a>b>0)的离心率e=
,a2与b2的等差中项为
.求:
(1)椭圆E的方程;
(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴交于点P(t,0),求实数t的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 13 |
| 2 |
(1)椭圆E的方程;
(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴交于点P(t,0),求实数t的取值范围.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由椭圆的离心率及a2与b2的等差中项为
列式求得a2,b2的值,则椭圆方程可求;
(2)设出椭圆上A,B两点的坐标,利用点差法求得AB的斜率,进一步得到AB的中垂线方程,求出与x轴交于点P的坐标,利用AB中点的坐标的范围得实数t的取值范围.
| 13 |
| 2 |
(2)设出椭圆上A,B两点的坐标,利用点差法求得AB的斜率,进一步得到AB的中垂线方程,求出与x轴交于点P的坐标,利用AB中点的坐标的范围得实数t的取值范围.
解答:
解:(1)由e=
=
,得
=
又a2+b2=13,
∴a2=9,b2=4,
∴椭圆E的方程为
+
=1;
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),则-3<x0<3,
∵A,B在椭圆上,则
+
=1,
+
=1,
作差可得,
=-
,即
=-
•
,
∴kAB=-
•
,
∴线段AB的垂直平分线方程为y-y0=
(x-x0),
取y=0得,t=
x0.
∴-
<t<
.
即实数t的取值范围是(-
,
).
| c |
| a |
| ||
| 3 |
| a2-b2 |
| a2 |
| 5 |
| 9 |
又a2+b2=13,
∴a2=9,b2=4,
∴椭圆E的方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),则-3<x0<3,
∵A,B在椭圆上,则
| x12 |
| 9 |
| y12 |
| 4 |
| x22 |
| 9 |
| y22 |
| 4 |
作差可得,
| (x1-x2)(x1+x2) |
| 9 |
| (y1-y2)(y1+y2) |
| 4 |
| y1-y2 |
| x1-x2 |
| 4 |
| 9 |
| x1+x2 |
| y1+y2 |
∴kAB=-
| 4 |
| 9 |
| x0 |
| y0 |
∴线段AB的垂直平分线方程为y-y0=
| 9y0 |
| 4x0 |
取y=0得,t=
| 5 |
| 9 |
∴-
| 5 |
| 3 |
| 5 |
| 3 |
即实数t的取值范围是(-
| 5 |
| 3 |
| 5 |
| 3 |
点评:本题考查了椭圆的简单几何性质,训练了利用点差法求与弦中点有关的问题,体现了数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
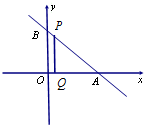 如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
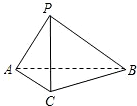 在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.