题目内容
已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=
,记椭圆和双曲线的离心率分别为e1,e2,则
+
的值为( )
| π |
| 3 |
| 1 |
| e12 |
| 3 |
| e22 |
| A、1 | B、2 | C、3 | D、4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设椭圆的长半轴长为a1,双曲线的半实轴长a2,焦距2c.因为涉及椭圆及双曲线离心率的问题,所以需要找a1,a2,c之间的关系,而根据椭圆及双曲线的定义可以用a1,a2表示出|PF1|,|PF2|,并且|F1F2|=2c,∠F1PF2=
,在△F1PF2中根据余弦定理可得到:
+
=4,所以
+
=4.
| π |
| 3 |
| a12 |
| c2 |
| 3a22 |
| c2 |
| 1 |
| e12 |
| 3 |
| e22 |
解答:
解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:
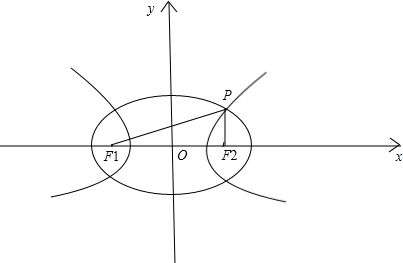
;
∴|PF1|=a1+a2,|PF2|=a1-a2,设|F1F2|=2c,∠F1PF2=
,则:
在△PF1F2中由余弦定理得,4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)•cos
;
∴化简得:a12+3a22=4c2,该式可变成:
+
=4;
∴
+
=4.
故选D.

|
∴|PF1|=a1+a2,|PF2|=a1-a2,设|F1F2|=2c,∠F1PF2=
| π |
| 3 |
在△PF1F2中由余弦定理得,4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)•cos
| π |
| 3 |
∴化简得:a12+3a22=4c2,该式可变成:
| a12 |
| c2 |
| 3a22 |
| c2 |
∴
| 1 |
| e12 |
| 3 |
| e22 |
故选D.
点评:考查椭圆及双曲线的交点,及椭圆与双曲线的定义,以及它们离心率的定义,余弦定理.

练习册系列答案
相关题目
为了得到函数y=sin(2x-
)的图象,可以将函数y=cos2x的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
方程
=|x+y+2|表示( )
| 2(x+1)2+2(y-1)2 |
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
函数f(x)=lgx-
的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
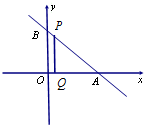 如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
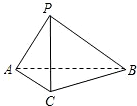 在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.