题目内容
过x轴正半轴上一点P的直线与抛物线y2=4x交于两点A、B，O是原点，A、B的横坐标分别为3和
，则下列：
①点P是抛物线y2=4x的焦点；
②
•
=-2；
③过A、B、O三点的圆的半径为
；
④若三角形OAB的面积为S，则
＜S＜
；
⑤若
=λ
，则λ=3．
在这五个命题中，正确的是 ．
| 1 |
| 3 |
①点P是抛物线y2=4x的焦点；
②
| OA |
| OB |
③过A、B、O三点的圆的半径为
| ||
| 3 |
④若三角形OAB的面积为S，则
| 9 |
| 4 |
| 7 |
| 3 |
⑤若
| AP |
| PB |
在这五个命题中，正确的是
考点：命题的真假判断与应用
专题：阅读型,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析：①设P（a，0），设直线方程，联立抛物线方程，消去y，得到二次方程，由两根之积，即可得到a；
②求出A，B的坐标，由向量的数量积的坐标表示，即可得到；
③运用两种方法求出三角形ABO的面积，注意面积公式S△ABC=
absinC=
；
④由△ABO的面积，即可判断；
⑤
=λ
，即
=λ
，由A，F，B的坐标，即可得到．
②求出A，B的坐标，由向量的数量积的坐标表示，即可得到；
③运用两种方法求出三角形ABO的面积，注意面积公式S△ABC=
| 1 |
| 2 |
| abc |
| 4R |
④由△ABO的面积，即可判断；
⑤
| AP |
| PB |
| AF |
| FB |
解答：
解：由图可得A（3，2
），B（
，-
）
①设P（a，0），过P的直线为y=k（x-a），联立抛物线方程消去y，得k2x2-（2ak2+4）x+k2a2=0，则3×
=a2，a=1，
即P（1，0）即为焦点F，故①对；
②
•
=（3，2
）•（
，-
）=3×
-2
×
=-3，
故②错；
③S△ABO=
×1×（2
+
）=
=
=
，R=
，故③对；
④S△ABO=
＞
，
＜
，故④对；
⑤若
=λ
，即
=λ
，λ=
=3，故⑤对．
故答案为：①③④⑤
解：由图可得A（3，2| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
①设P（a，0），过P的直线为y=k（x-a），联立抛物线方程消去y，得k2x2-（2ak2+4）x+k2a2=0，则3×
| 1 |
| 3 |
即P（1，0）即为焦点F，故①对；
②
| OA |
| OB |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
故②错；
③S△ABO=
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
| AB•OA•OB |
| 4R |
=
| ||||||||
| 4R |
| ||
| 3 |
④S△ABO=
4
| ||
| 3 |
| 9 |
| 4 |
4
| ||
| 3 |
| 7 |
| 3 |
⑤若
| AP |
| PB |
| AF |
| FB |
| 1-3 | ||
|
故答案为：①③④⑤
点评：本题考查抛物线的定义、性质和方程，考查直线方程和抛物线方程联立，消去未知数，得到二次方程，应用韦达定理求解，同时考查平面向量的数量积的坐标表示，和向量共线定理，以及求外接圆的半径应用面积公式，属于中档题．
练习册系列答案
相关题目
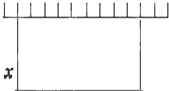某工厂需要建一个面积为512m2的矩形堆料场，一边可以利用原有的墙壁，为了使砌墙所用的材料最省，则图中的x=