题目内容
解关于x的不等式:ax2+(2a-1)x-2>0(a<0).
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:对a与-
的大小关系分类讨论,利用一元二次不等式的解法即可得出.
| 1 |
| 2 |
解答:
解:当a<0时,原不等式可化为(x-
)(x+2)<0,
当
>-2,即a<-
时,不等式(x-
)(x+2)<0的解集为{x|-2<x<
};
当
=-2,即a=-
时,不等式(x-
)(x+2)<0化为(x+2)2<0,其解集为∅;
当
<-2,即-
<a<0时,不等式(x-
)(x+2)<0的解集为{x|
<x<-2}.
综上所述:当
>-2,不等式的解集为{x|-2<x<
};
当
=-2,不等式的解集为∅;
当
<-2,不等式的解集为{x|
<x<-2}.
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
综上所述:当
| 1 |
| a |
| 1 |
| a |
当
| 1 |
| a |
当
| 1 |
| a |
| 1 |
| a |
点评:本题考查了一元二次不等式的解法,考查了分类讨论的思想方法,属于中档题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
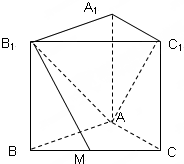 如图,正三棱柱ABC-A1B1C1中,点M是BC的中点,AB=2,BB1=
如图,正三棱柱ABC-A1B1C1中,点M是BC的中点,AB=2,BB1=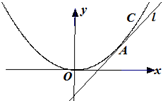 如图,直线l:y=x+b与曲线C:x2=4y相切于点A.
如图,直线l:y=x+b与曲线C:x2=4y相切于点A.