题目内容

写出函数y=sin（2x-
π
6
）的单调递减区间．
考点：复合三角函数的单调性
专题：三角函数的图像与性质
分析：直接由正弦型复合函数的单调性求解原函数的单调减区间．
解答： 解：由
π
2
+2kπ≤2x-
π
6
≤
3π
2
+2kπ，得
π
3
+kπ≤x≤
5π
6
+kπ，k∈Z．
∴函数y=sin（2x-
π
6
）的单调递减区间为[
π
3
+kπ，
5π
6
+kπ]，k∈Z．
点评：本题考查了复合三角函数的单调性，复合函数的单调性满足同增异减的原则，是基础题．
练习册系列答案
相关题目
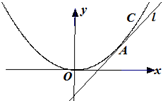如图，直线l：y=x+b与曲线C：x2=4y相切于点A．
（Ⅰ）求实数b的值；
（Ⅱ）求由曲线C与直线l及x=0围成的图形的面积．
解关于x的不等式（ax-1）（x-1）＜0．
（1）点M（x，y）到定点F（5，0）的距离和它到定直线l：x=
16
5
的距离的比是常数
5
4
，求点M的轨迹．
（2）已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心C在直线l：x-y+1=0上，求圆心为C的圆的标准方程．
已知函数y=cos（2x+
π
3
）．
（1）用“五点法”作出它在长度为一个周期的闭区间上的简图；（自己做出坐标系，并标出横纵坐标）
（2）求使函数y取最大值和最小值时自变量x的集合，并求出它的最大值和最小值；
（3）指出该函数的增区间和减区间．
过x轴正半轴上一点P的直线与抛物线y2=4x交于两点A、B，O是原点，A、B的横坐标分别为3和
1
3
，则下列：
①点P是抛物线y2=4x的焦点；
②
OA
•
OB
=-2；
③过A、B、O三点的圆的半径为
91
3
；
④若三角形OAB的面积为S，则
9
4
＜S＜
7
3
；
⑤若
AP
=λ
PB
，则λ=3．
在这五个命题中，正确的是
 
．
在椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）中，当离心率e趋近于0时，短半轴b就趋近于长半轴a，此时椭圆就趋近于圆．类比圆的面积公式，在椭圆中，S椭=
 
．
（x+2）4展开式中含x项的系数等于
 
．
已知随机变量ξ服从正态分布N（2，σ2），P（ξ≥4）=0.4，则P（ξ≤0）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网