题目内容
已知矩阵M=
,a=
.
(1)求矩阵M的逆矩阵M-1;
(2)求矩阵M的特征值和特征向量;
(3)试计算M20a;.
|
|
(1)求矩阵M的逆矩阵M-1;
(2)求矩阵M的特征值和特征向量;
(3)试计算M20a;.
考点:特征值与特征向量的计算
专题:矩阵和变换
分析:本题(1)利用逆矩阵的公式可求出矩阵M的逆矩阵;(2)利用矩阵的特征多项式求出矩阵的特征值,利用对应方程组求出相应的特征向量;(3)将向量分解成两个特征向量的线性和,再利用特征向量的定义得出矩阵与向量和积,得到本题结论.
解答:
解:(1)|M|=-3,由逆矩阵公式知M-1=
.
(2)矩阵M的特征多次式为f(λ)=
=(λ-1)2-4
令f(λ)=0,得λ1=3,λ2=-1,
当λ1=3时,
,取x=1,则y=-1,对应的特征向量为
;
当λ2=-1,时,
,取x=1,则y=1,对应的特征向量为
.
∴矩阵M的特征值为λ1=3,λ2=-1,对应的特征向量分别为
和
.
(3)α=
=
+2
,
∴M20α=320
+2(-1)20
=
.
|
(2)矩阵M的特征多次式为f(λ)=
|
令f(λ)=0,得λ1=3,λ2=-1,
当λ1=3时,
|
|
当λ2=-1,时,
|
|
∴矩阵M的特征值为λ1=3,λ2=-1,对应的特征向量分别为
|
|
(3)α=
|
|
|
∴M20α=320
|
|
|
点评:本题考查的是逆矩阵的求法,可以用定义法或公式法,本题还考查了矩阵的特征值和特征向量及其应用,有一定的思维难度,计算量较大,属于中档题.

练习册系列答案
相关题目
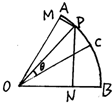 如图,扇形OAB的半径为2,圆心角为
如图,扇形OAB的半径为2,圆心角为