题目内容
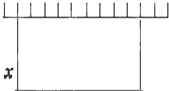某工厂需要建一个面积为512m2的矩形堆料场，一边可以利用原有的墙壁，为了使砌墙所用的材料最省，则图中的x=考点：基本不等式
专题：不等式的解法及应用
分析：本题可以先建立面积关于x的函数，再通过求函数的最值问题得到本题答案．
解答：
解：∵堆料场是一个面积为512m2的矩形，一边长为x m，
∴邻边长为
m．
∵一边可以利用原有的墙壁，
∴需要砌墙的三边长之和为：y=2x+
（单位m），
y=2x+
≥2
=64，
当且仅当2x=
，即x=16时，函数取最小值．
故答案为16．
∴邻边长为
| 512 |
| x |
∵一边可以利用原有的墙壁，
∴需要砌墙的三边长之和为：y=2x+
| 512 |
| x |
y=2x+
| 512 |
| x |
2x•
|
当且仅当2x=
| 512 |
| x |
故答案为16．
点评：本题是一道不等式应用题，考查了数学建模和基本不等式的知识，本题思维难度不大，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目