题目内容
15.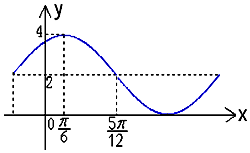 函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.
函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.(1)求函数y=f(x)解析式;
(2)求x∈[0,$\frac{π}{2}$]时,函数y=f(x)的值域;
(3)将函数y=f(x)的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=g(x)的图象,求函数y=g(x)的单调递减区间.
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)利用正弦函数的定义域和值域,求得x∈[0,$\frac{π}{2}$]时,函数y=f(x)的值域.
(3)利用正弦函数的单调性,求得函数y=g(x)的单调递减区间.
解答 解:(1)根据函数f(x)=Asin(ωx+ϕ)+B的一部分图象,其中A>0,ω>0,|φ|<$\frac{π}{2}$,
可得A=4-2=2,B=2,$\frac{T}{4}$=$\frac{1}{4}•\frac{2π}{ω}$=$\frac{5π}{12}$-$\frac{π}{6}$,∴ω=2.
再根据五点法作图,可得2•$\frac{π}{6}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{6}$,∴f(x)=2sin(2x+$\frac{π}{6}$)+2.
(2)∵x∈[0,$\frac{π}{2}$],∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],∴y=f(x)∈[1,4].
(3)将函数y=f(x)的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=g(x)=2sin[2(x-$\frac{π}{4}$)+$\frac{π}{6}$]+2=2sin(2x-$\frac{π}{3}$)+2的图象,
对于函数y=g(x)=2sin(2x-$\frac{π}{3}$)+2,令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$,
故函数g(x)的单调增区间为[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.还考查了正弦函数的定义域和值域,正弦函数的单调性,属于中档题.

| A. | 向左平移$\frac{π}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向左平移$\frac{π}{10}$个单位长度 | D. | 向右平移$\frac{π}{10}$个单位长度 |
| A. | 0 | B. | 0 或1 | C. | 1 | D. | 0 或1或-1 |
 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.