题目内容
14.函数y=f(x),x∈D,若常数C满足C>0,且函数y=f(x)在x∈D上的值域是y=$\frac{C^2}{f(x)}$,在x∈D上的值域的子集,则称函数f(x)在D上的几何平均数为C.(1)已知f(x)=lnx,求函数f(x)在[e,e2]上的几何平均数;
(2)若函数f(t)=-2t2-at+1(a<-1)在区间[$\frac{1}{2}$,1]上的几何平均数为$\frac{{\sqrt{{a^2}+8}}}{2}$,求实数a的值.
分析 (1)根据新定义,值域是y=$\frac{C^2}{f(x)}$在x∈D上的值域的子集,则称函数f(x)在D上的几何平均数为C.
令y=f(x1),则$f({x}_{1})•f({x}_{2})={C}^{2}$,我们易得若函数在区间D上单调递增,则C应该等于函数在区间D上最大值与最小值的几何平均,求解即可.
(2)根据对称轴讨论二次函数的最值,C应该等于函数在区间D上最大值与最小值的几何平均,求解即可.
解答 解:根据新定义,关于函数f(x)在D上的几何平均数为C的定义,
结合f(x)=lnx,在区间[e,e2]上单调递增
则x1=e时,存在唯一的x2=e2与之对应
故CC2=lne×lne2=2,
∵C>0,
故得C=$\sqrt{2}$
即函数f(x)在[e,e2]上的几何平均数C=$\sqrt{2}$.
(2)函数f(t)=-2t2-at+1(a<-1),
其对称轴t=$-\frac{a}{4}$,图象开口向下,
当$-\frac{a}{4}≤\frac{1}{2}$或$-\frac{a}{4}≥1$时,即-1>a≥-2或a≤-4,
t在区间$[\frac{1}{2},1]$上单调,
则x1=$\frac{1}{2}$时,存在唯一的x2=1与之对应,
根据已知中关于函数f(x)在D上的几何平均数为C的定义,
几何平均数C=f($\frac{1}{2}$)•f(1)=$-\frac{1}{2}(1-a)(1+a)$
即$-\frac{1}{2}(1-a)(1+a)$=$\frac{{\sqrt{{a^2}+8}}}{2}$,
此时a不满题意.
当$\frac{1}{2}$≤$-\frac{a}{4}≤1$时,即-1>a≥-4.
此时的最大值为f($-\frac{a}{4}$)=$\frac{{a}^{2}+8}{8}$,最小值为f($\frac{1}{2}$)或f(1).
几何平均数C2=f($\frac{1}{2}$)•f($-\frac{a}{4}$)=$\frac{{a}^{2}+8}{4}$或几何平均数C2=f($-\frac{a}{4}$)•f(1)=$\frac{{a}^{2}+8}{4}$
此时a=$-\sqrt{3}$或a=3,满足题意.
故得函数f(t)=-2t2-at+1(a<-1)在区间[$\frac{1}{2}$,1]上的几何平均数为$\frac{{\sqrt{{a^2}+8}}}{2}$,实数a的值为$-\sqrt{3}$或-3.
点评 本题考查了对新定义的理解和运用,以及二次函数的最值的讨论与新定义法结合的化简与计算.属于中档题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案| A. | 5或6个 | B. | 3或9个 | C. | 9或10个 | D. | 5或9个 |
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下:
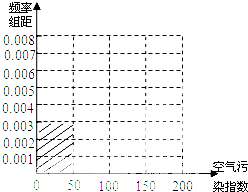
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
| A. | $\frac{9}{13}$ | B. | $\frac{5}{7}$ | C. | $\frac{17}{25}$ | D. | 1 |
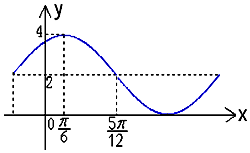 函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.
函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.